| Excerpt |
|---|
|
A version of the ballistic pendulum problem in which rotational effects are important. |
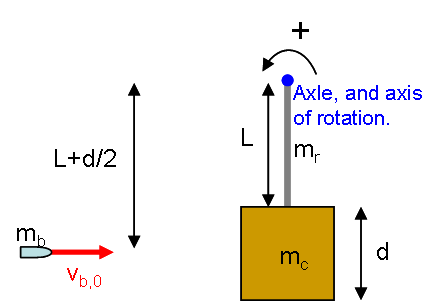
Suppose that a very simple ballistic pendulum is made by attaching a 2.5 kg solid wooden cube 0.17 m on each side to a 0.25 m long metal rod with a mass of 0.75 kg. The rod is attached to the block in the center of one of the faces. The assembled pendulum (rod plus block) is hung straight down from a smooth axle so that the block is at the bottom. The pendulum can rotate freely about the axle. A 4.0 g bullet moving perfectly horizontally (and perpendicular to the axle) at 920 m/s strikes the block in the center of one of the faces. The bullet embeds itself in the exact center of the block. What is the angular speed of the entire system about the axle immediately after the collision?
Solution
System: | Cloak |
|---|
|
Bullet plus pendulum.
|
Interactions: | Cloak |
|---|
|
Angular impulse from gravity is neglected under the assumption that the collision is instantaneous, while angular impulse from the axle is neglected because we have chosen the axle as the axis of rotation. intdeck Internal
| The internal forces are very large, but their torques
cancel by Newton's third law. |
External
| The external forces from gravity are too small to produce
significant impluse during the rapid collision. The axle
force is large enough to produce a significant impulse,
but it is applied at the axis of rotation and so produces
zero torque. |
The linear impulse from the axle is not negligible even though the collision is very rapid. For this reason we must use angular momentum, which allows us to set the torque from the axle to zero by choosing the axle as the rotation axis. A good way to understand why the force from the axle is important during the collision is to think about how the collision proceeds in terms of linear momentum. When the bullet hits the block, the block tries to move to the right (conserving linear momentum), but it immediately "collides" with the axle, which causes the pendulum to rotate rather than simply translating. Why can we ignore the linear impulse from the axle force and so conserve linear momentum if the rod is replaced by a string? (Hint: can a string "collide" with the axle in the same way as a rod? Consider how a string behaves under side impact...) |
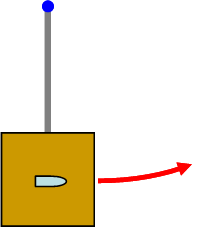
Model: Approach: Diagrammatic Representation We first construct an initial-state final-state diagram of the situation.
|
|
Initial State | Final State |
|---|
The presence of the axle dictates that the final state will be in pure rotation, provided that we choose to consider rotations about the axis defined by the axle. We make this choice of axis, which then allows us to ignore linear momentum and focus only on angular momentum. The angular momentum is conserved in the limit that we neglect external torques during the collision.
To use conservation of angular momentum, we must be able to find the angular momentum of each system constituent before and after the collision. Before the collision, the system consists of a translating point particle (the bullet) and a stationary rigid body. The pendulum clearly contributes nothing to the angular momentum in the initial state. The bullet, since it is not purely rotating about the axle, contributes:
| Latex |
|---|
\begin{large}\[L_{b,i} = m_{b}v_{b,i}(L+d/2) + I_{b,cm}\omega_{b,cm} = m_{b}v_{b,i}(L+d/2) \]\end{large} |
where we have assumed that the bullet's moment of inertia about its own center of mass is negligible (the bullet is taken to be a point particle).
In the final state, the bullet has joined the pendulum to form a composite object. The composite object will have:
| Latex |
|---|
\begin{large}\[L_{f} = (I_{b,a} + I_{p,a})\omega_{f} = (m_{b}(L+d/2)^{2} + I_{p,a})\omega_{f}\]\end{large} |
where Ib,a is the moment of inertia of the bullet with respect to the axis of rotation and Ip,a is the moment of inertia of the original pendulum (without the bullet) about the axis of rotation. In coming to the final form, we have again assumed the bullet is a point particle and use the expression for the moment of inertia of a point particle.
Using the fact that the angular momentum is approximately constant during the collision, we can now write:
| Latex |
|---|
\begin{large}\[ (m_{b}(L+d/2)^{2} + I_{p}) \omega_{\rm f} = m_{b}v_{b,{\rm i}}(L+d/2)\]\end{large} |
To use this equation to find the final angular speed, we must first determine the moment of inertia of the pendulum. The pendulum is composed of two parts: a rod (assumed thin) rotated about one end and a block rotated about an axis displaced by a distance L+d/2 from its center of mass. The contribution of the rod is a standard one:
| Latex |
|---|
\begin{large}\[ I_{r} = \frac{1}{3} m_{r}L^{2} \]\end{large} |
To get the contribution of the cubic block we must use the parallel axis theorem:
| Latex |
|---|
\begin{large}\[ I_{c} = I_{c,cm} + m_{c}(L+d/2)^{2} = \frac{1}{12}m_{c}(d^{2}+d^{2}) + m_{c}(L+d/2)^{2} = \frac{1}{6}m_{c}d^{2}+m_{c}(L+d/2)^{2}\]\end{large} |
We therefore know that:
| Latex |
|---|
\begin{large}\[ I_{p} = I_{r} + I_{c} = \frac{1}{3}m_{r}L^{2} +\frac{1}{6}m_{c}d^{2} + m_{c}(L+d/2)^{2})\]\end{large} |
Inputting into the conservation of momentum equation and solving for ω, we find:
| Latex |
|---|
\begin{large}\[ \omega_{\rm f} = \frac{m_{b}v_{b,{\rm i}}(L+d/2)}{m_{b}(L+d/2)^{2} + \frac{1}{3}m_{r}L^{2}+ \frac{1}{6}m_{c}d^{2}+m_{c}(L+d/2)^{2}} =\left(\frac{1}{L+d/2}\right)\frac{m_{b}v_{b,{\rm i}}}{m_{b}+ m_{c} + \frac{1}{3}m_{r}\frac{\displaystyle L^{2}}{\displaystyle (L+d/2)^{2}} + \frac{1}{6}m_{c}\frac{\displaystyle d^{2}}{\displaystyle (L+d/2)^{2}}}\]\end{large} |
| Tip |
|---|
You should check that by taking the simultaneous limits:
| Latex |
|---|
\[ d << L \qquad \mbox{and} \qquad m_{r} << m_{c}\] |
the expression turns into the result obtained using linear momentum alone. (In these simultaneous limits, the rod has no inertia at all and the block becomes a point mass that has no resistance to rotation.) |
| Wiki Markup |
|---|
{html}
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>
{html} |

