U(r) = U(\infty) - \lim_{r_{0}\rightarrow \infty}\int_{r_{0}}^{r} \left(-G\frac{m_{1}m_{2}}{r^{2}}\right) \;dr
= - Gm_{1}m_{2} \left(\frac{1}{r}-\lim_{r_{0}\rightarrow \infty}\frac{1}{r_{0}}\right)\]
\[U(r) = -G\frac{m_{1}m_{2}}{r} \]\end{large} |
Potential Energy CurveIf the two objects are isolated from other influences, their potential energy curve is then: 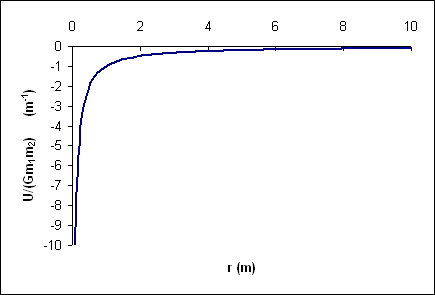 Image Added Image Added
This potential energy curve is somewhat misleading, since the potential is spherically symmetric. Thus, although in spherical coordinates, r cannot go negative, if we define a one-dimensional coordinate system by following a radial line through the origin (suppose, for instance, we chose to follow the z axis where z = r cosθ) we would generate a curve: 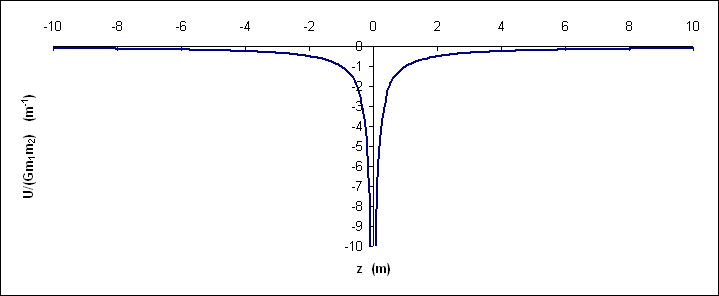 Image Added Image Added
which indicates the possibility of stable equilibrium when the objects' separation goes to zero. Of course, this is technically impossible for objects of finite size. Gravitational Potential Energy of a SystemIn a system composed of many spherically symmetric objects, the total gravitational potential energy can be found by adding up the contribution from each distinct interaction. It is very important to note that any pair of the bodies experiences only one interaction between them. Take, for example, a system composed of four objects labeled 1, 2, 3 and 4. There are six distinct interactions among these bodies, each of which has an associated potential energy: | 
