h2. Part C Image Added Image Added
A person is trying to lift a 10 kg box by applying a perfectly vertical force of 20 N with the help of a pulley. What is the magnitude of the normal force exerted on the box by the floor? Solution System: Interactions: | Cloak |
|---|
| External influences from the earth (gravity), the floor (normal force) and the rope (tension). |
Model: Approach: Diagrammatic Representation We begin with a free body diagram for the box: 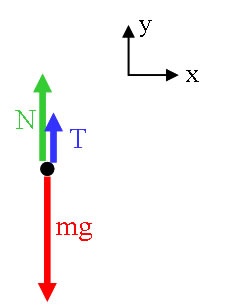 Image Added Image Added
Mathematical Representation From the free body diagram, we can write the equations of Newton's 2nd Law. We ignore the x-direction, since there are no forces acting. | Latex |
|---|
C
!normalbox3.png|width=40%!
A person is trying to lift a 10 kg box by applying a perfectly vertical force of 20 N with the help of a pulley. What is the magnitude of the normal force exerted on the box by the floor?
h4. Solution
{toggle-cloak:id=sysc} *System:* {cloak:id=sysc}Box as [point particle].{cloak}
{toggle-cloak:id=intc} *Interactions:* {cloak:id=intc}External influences from the earth (gravity), the floor (normal force) and the rope (tension).{cloak}
{toggle-cloak:id=modc} *Model:* {cloak:id=modc}[Point Particle Dynamics].{cloak}
{toggle-cloak:id=appc} *Approach:*
{cloak:id=appc}
{toggle-cloak:id=diagc} {color:red} *Diagrammatic Representation* {color}
{cloak:id=diagc}
We begin with a free body diagram for the box:
!normalfbd3.jpg!
{cloak:diagc}
{toggle-cloak:id=mathc} {color:red} *Mathematical Representation* {color}
{cloak:id=mathc}
From the free body diagram, we can write the equations of [Newton's 2nd Law|Newton's Second Law]. We ignore the x-direction, since there are no forces acting.
{latex}\begin{large}\[ \sum F_{y} = T + N - mg = ma_{y}\]\end{large}{latex}
|
Because the box is sliding over level ground, it is not moving at all in the _y _ direction. Thus, it certainly has no y-acceleration. Setting _a _~y~ y = 0 in the _y _ direction equation gives:
{| Latex |
|---|
}\begin{large}\[ T + N - mg = 0 \]\end{large}{latex}
| Solving for the normal force gives:
{| Latex |
|---|
}\begin{large}\[ N = mg - T = \mbox{78 N}\]\end{large}{latex}
{tip}When three or more forces act in a direction with zero acceleration, it is always a good idea to check your answer by putting the numbers on the free body diagram and making sure that they balance. In this case, T (20 N) and N (78 N) act to balance mg (98 N).{tip}
{note}Follow up question: The floor no longer supports the entire weight of the box (98 N) because the rope is carrying some of the weight (20 N). How will the _person's_ normal force be affected in this situation? If the floor is carrying so much less weight, what part of the building is now feeling an extra load?{note}
{cloak:mathc}
{cloak:appc}
| | Tip |
|---|
When three or more forces act in a direction with zero acceleration, it is always a good idea to check your answer by putting the numbers on the free body diagram and making sure that they balance. In this case, T (20 N) and N (78 N) act to balance mg (98 N). |
| Note |
|---|
Follow up question: The floor no longer supports the entire weight of the box (98 N) because the rope is carrying some of the weight (20 N). How will the person's normal force be affected in this situation? If the floor is carrying so much less weight, what part of the building is now feeling an extra load? |
|