{excerpt}An interaction between two massive particles resulting in an attractive force exerted on each by the other. The force is proportional to the gravitational constant G={{{*}6.674 28(67) x 10{*}{*}^\-11{^}* *m{*}{*}{^}3{^}{*}* kg{*}{*}^\-1{^}{*}* s{*}{*}^\-2{^}{*}}}, and the masses of the bodies, and inversely proportional to the square of the distance between them.{excerpt}
|| Page Contents ||
| {toc:indent=10px|style=none} |
----
h2. Motivation for Concept
Newton's Law of Universal Gravitation provides an effective description of the movement of objects from submillimeter distances to galactic sizes, and is the dominant force on most macroscopic objects near the earth and in the solar system.
----
h2. Newton's Law of Universal Gravitation
h4. Statement of the Law for Point Masses
Between any two massive bodies (masses _m{_}{~}1~ and _m{_}{~}2~, respectively) there will exist an attractive force. The force on body 1 due to body 2 will have the form:
{latex}| Table Row (tr) |
|---|
| | Table Cell (td) |
|---|
| Excerpt |
|---|
An interaction between two massive particles resulting in an attractive force exerted on each by the other. The force is proportional to the gravitational constant G = 6.674 28(67) x 10-11 m3 kg-1 s-2, and the masses of the bodies, and inversely proportional to the square of the distance between them. |
Motivation for ConceptNewton's Law of Universal Gravitation provides an effective description of the movement of objects from submillimeter distances to galactic sizes, and is the dominant force on most (macroscopic) astronomical bodies. Gravitational Force (Newton's Law of Universal Gravitation)Statement of the Law for Point MassesBetween any two point masses (masses m1 and m2, respectively) there will exist an attractive force along the line joining the masses. The force on body 1 due to body 2 will have the form: |
|
\begin{large}\[ \vec{F}_{12} = - G \frac{m_{1}m_{2}}{r_{12}^{2}} \hat{r}_{12} \]\end{large} |
|
|
{latex}
where _r{_}{~}12~ is the position vector of object 1 in a coordinate system with object 2 located at the origin and _G_ is a constant of proportionality equal to:
{latex}where, G is the gravitational constant equal to: | Latex |
|---|
\begin{large}\[ G = \mbox{6.67}\times\mbox{10}^{-11}\mbox{ N}\frac{\mbox{m}^{2}}{\mbox{kg}^{2}} \]\end{large} |
r12 is the distance between the two objects and is obtained as the magnitude of the vector difference between the position vector of object 1 and the position vector of object 2. The vector difference is expressed as:
| Latex |
|---|
\begin{large}\[\vec{r}_{ |
|
|
latex}
h4. Compatibility with Newton's Laws of Motion
Note that the Universal Law of Gravity is consistent with Newton's [Third Law of Motion|Newton's Third Law]:
{latex}12} = \vec{r}_{1}-\vec{r}_{2}\]\end{large} |
Compatibility with Newton's Laws of MotionNote that the Universal Law of Gravition is consistent with Newton's Third Law of Motion:
| Latex |
|---|
\begin{large}\[ \vec{F}_{21} = -G\frac{m_{2}m_{1}}{r_{21}^{2}} \hat{r}_{21}\]\end{large} |
|
|
{latex}
_r{_}{~}12~ and _r{_}{~}21~ will certainly satisfy:
{latex} r12 and r21 will certainly satisfy:
| Latex |
|---|
\begin{large}\[ \vec{r}_{12} = - \vec{r}_{21}\]\end{large} |
|
|
{latex}
{} |
|---|
\begin{large}\[ \vec{F}_{12} = - \vec{F}_{21}\]\end{large} |
|
|
{latex}
h4. The Case of Spherical Symmetry
Although the form of the Law of Universal Gravitation is strictly valid only for [point particles|point particle], it is possible to show that for extended objects with a spherically symmetric mass distribution, the Law will hold in the form stated above *provided that the positions of the spherical objects are specified by their centers*.
----
h2. Gravitational Potential Energy
h4. Form of the Potential Energy
For two spherically symmetric objects (objects 1 and 2), it is customary to analyze the energy of the gravitational interaction by constructing spherical coordinates with one of the objects at the origin (if one of the objects dominates the mass of the system, its position is typically used as the origin). Newton's Law of Universal Gravitation then takes the form:
{latex}The Case of Spherical SymmetryAlthough the form of the Law of Universal Gravitation is strictly valid only for point particles, it is possible to show that for extended objects with a spherically symmetric mass distribution, the Law will hold in the form stated above provided that the positions of the spherical objects are specified by their centers. Gravitational Potential EnergyFor two spherically symmetric objects (objects 1 and 2), it is customary to analyze the energy of the gravitational interaction by constructing spherical coordinates with one of the objects at the origin (if one of the objects dominates the mass of the system, its position is typically used as the origin). Newton's Law of Universal Gravitation then takes the form: | Latex |
|---|
\begin{large}\[ \vec{F} = - G\frac{m_{1}m_{2}}{r^{2}} \hat{r}\]\end{large} |
|
|
{latex}
where _r_ is the position of the object that is not placed at the origin.
It is also customary to make the assignment that the potential energy of the system goes to zero as the separation goes to infinty:
{latex}where r is the position of the object that is not placed at the origin. It is also customary to make the assignment that the potential energy of the system goes to zero as the separation goes to infinty: | Latex |
|---|
\begin{large}\[ \lim_{r \rightarrow \infty} U(r) = 0 \]\end{large} |
|
|
{latex}
__
{} |
|---|
\begin{large}\[ U(r) = U(\infty) - \lim_{r_{0}\rightarrow \infty}\int_{r_{0}}^{r} \left(-G\frac{m_{1}m_{2}}{r^{2}}\right) \;dr
= - Gm_{1}m_{2} \left(\frac{1}{r}-\lim_{r_{0}\rightarrow \infty}\frac{1}{r_{0}}\right)\]
\[U(r) = -G\frac{m_{1}m_{2}}{r} \]\end{large} |
|
|
{latex}
h4. Potential Energy Curve
If the two objects are isolated from other influences, their potential energy curve is then:
!uvsr.gif!
This potential energy curve is somewhat misleading, since the potential is spherically symmetric. Thus, although in spherical coordinates, _r_ cannot go negative, if we define a one-dimensional coordinate system by following a radial line through the origin (suppose, for instance, we chose to follow the _z_ axis where _z_ = _r{_}cosθ) we would generate a curve:
!uvsz.gif!
which indicates the possibility of stable equilibrium when the objects' separation goes to zero. Of course, this is technically impossible for objects of finite size.
h4. Gravitational Potential Energy of a System
In a system composed of many spherically symmetric objects, the total gravitational potential energy can be found by adding up the contribution from each distinct _interaction_.
It is very important to note that any pair of the bodies experiences only one interaction between them. Take, for example, a system composed of four objects labeled 1, 2, 3 and 4. There are six distinct interactions among these bodies, each of which has an associated potential energy:
{latex}Potential Energy CurveIf the two objects are isolated from other influences, their potential energy curve is then: 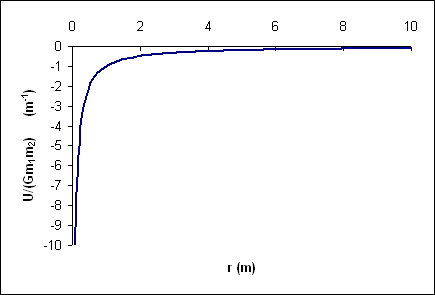 Image Added Image Added
This potential energy curve is somewhat misleading, since the potential is spherically symmetric. Thus, although in spherical coordinates, r cannot go negative, if we define a one-dimensional coordinate system by following a radial line through the origin (suppose, for instance, we chose to follow the z axis where z = r cosθ) we would generate a curve: 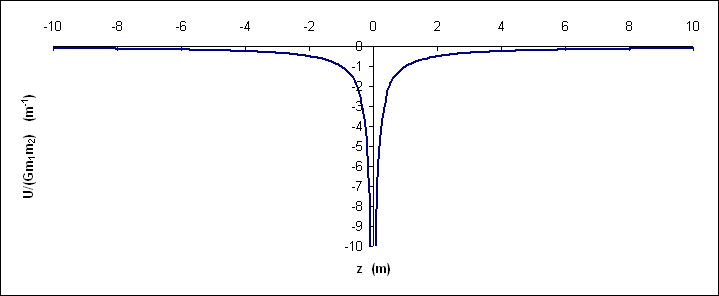 Image Added Image Added
which indicates the possibility of stable equilibrium when the objects' separation goes to zero. Of course, this is technically impossible for objects of finite size. Gravitational Potential Energy of a SystemIn a system composed of many spherically symmetric objects, the total gravitational potential energy can be found by adding up the contribution from each distinct interaction. It is very important to note that any pair of the bodies experiences only one interaction between them. Take, for example, a system composed of four objects labeled 1, 2, 3 and 4. There are six distinct interactions among these bodies, each of which has an associated potential energy: | Latex |
|---|
\begin{large}\[ 1 \leftrightarrow 2 \mbox{ gives rise to }U_{12}\]
\[ 1 \leftrightarrow 3 \mbox{ gives rise to }U_{13}\]
\[ 1 \leftrightarrow 4 \mbox{ gives rise to }U_{14}\]
\[ 2 \leftrightarrow 3 \mbox{ gives rise to }U_{23}\]
\[ 2 \leftrightarrow 4 \mbox{ gives rise to }U_{24}\]
\[ 3 \leftrightarrow 4 \mbox{ gives rise to }U_{34}\]\end{large} |
|
|
{latex}
{} |
|---|
\begin{large}\[ U_{\rm sys} = U_{12}+U_{13}+U_{14}+U_{23}+U_{24}+U_{34}\]\end{large} |
|
|
{latex}
{warning}It is important to beware of the temptation to | Warning |
|---|
It is important to beware of the temptation to double-count. |
|
|
__~12~ __ both object 2.{warning}
----
h2. Gravity Near Earth's Surface
h4. Defining "Near"
Suppose an object of mass _m_ is at a height _h_ above the surface of the earth. Assume that the earth is spherical with radius _R{_}{~}E~. Working in spherical coordinates the origin at the center of the earth, the gravitational force on the object from the earth will be:
{latex}\begin{large}\[ \vec{F} = - G \frac{M_{E}m}{(R_{E}+h)^{2}} \hat{r} \]\end{large}{latex}
A Taylor expansion gives:
{latex}\begin{large}\[ \vec{F} \approx - G \frac{M_{E}m}{R_{E}^{2}}\left(1 - 2\frac{h}{R_{E}} + ...\right)\hat{r} \]\end{large}{latex}
Thus, for _h_/_R{_}{~}E~ << 1, the gravitational force from the earth on the will be essentially independent of altitude above the earth's surface and will have a magnitude equal to:
{latex}\begin{large}\[ F_{g} = mG\frac{M_{E}}{R_{E}^{}} \]\end{large}{latex}
h4. Defining _g_
The above expression is of the form:
{latex}\begin{large}\[ F_{g} = mg \]\end{large}{latex}
if we take:
{latex}\begin{large}\[ g = G\frac{M_{E}}{R_{E}^{2}} = \left(6.67\times 10^{-11}\mbox{ N}\frac{\mbox{m}^{2}}{\mbox{kg}^{2}}\right)\left(\frac{5.98\times 10^{24}\mbox{ kg}}{(6.37\times 10^{6}\mbox{ m})^{2}}\right) = \mbox{9.8 m/s}^{2}\]\end{large}{latex}
h4. Gravitational Potential Energy Near Earth
Near the earth's surface, if we assume coordinates with the +{_}y_ direction pointing upward, the force of gravity can be written:
{latex}\begin{large}\[ \vec{F} = -mg \hat{y}\]\end{large}{latex}
Since the "natural" ground level varies depending upon the specific situation, it is customary to specify the coordinate system such that:
{latex}\begin{large}\[ U(0) \equiv 0\]\end{large}{latex}
The [gravitational potential energy] at any other height _y_ can then be found by choosing a path for the work integral that is perfectly vertical, such that:
{latex}\begin{large}\[ U(y) = U(0) - \int_{0}^{y} (-mg)\;dy = mgy\]\end{large}{latex}
For an object in vertical freefall (no horizontal motion) the associated potential energy curve would then be:
POTENTIAL ENERGY CURVE
For movement under pure near-earth gravity, then, there is no equilibrium point. At least one other force, such as a normal force, tension, etc., must be present to produce equilibrium.
|

