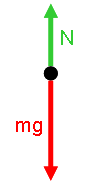| Excerpt |
|---|
|
Finding apparent weight using normal force. |
| Composition Setup |
|---|
cloak.memory.duration = 0
|
One way that we perceive weight is the normal force we experience from the ground. In physics problems, when you are asked to determine apparent weight, the quickest method is usually to compute the normal force provided by the "ground".
...
| Deck of Cards |
|---|
|
| Card |
|---|
| unmigrated-wiki-markup |
h2. Part A
Suppose a person with a weight of 686 N is in an elevator which is descending at a constant rate of 1.0 m/s and speeding up at a rate of is accelerating downwards at a rate of 3.0 m/s {color:black}^2^{color}. What is the 2. What is the person's apparent weight?
h4. Solution
{Solution:=} * System: Interactions: | Cloak |
|---|
| External influences from the earth (gravity) and the floor of the elevator (normal force). |
Model: Approach: Diagrammatic RepresentationsThe physical picture and free body diagram for the person is: 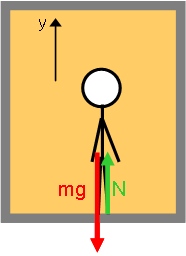 Image Added Image Added | 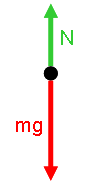 Image Added Image Added | Physical Picture | Free Body Diagram |
|---|
which leads to the form of Newton's 2nd Law for the y direction: | Latex |
|---|
* {cloak:id=Asys}Person as a [point particle].{cloak}
{toggle-cloak:id=Aint} *Interactions:* {cloak:id=Aint}External influences from the earth (gravity) and the floor of the elevator (normal force).{cloak}
{toggle-cloak:id=Amod} *Model:* {cloak:id=Amod}[Point Particle Dynamics].{cloak}
*Approach:* The physical picture and free body diagram for the person is:
|!Apparently I've Lost Weight^elevator1.png!|!elevator2.png!|
||Physical Picture||Free Body Diagram||
which leads to the form of [Newton's 2nd Law|Newton's Second Law] for the _y_ direction:
{latex}\begin{large}\[ \sum F_{y} = N - mg = ma_{y} \]\end{large}{latex}
|
In our coordinates, the acceleration of the person is _a _~y~ y = -3.0 m/s2, giving: | Latex |
|---|
{color:black}^2^{color}, giving:
{latex}\begin{large}\[ N = ma_{y} + mg = \mbox{476 N} \]\end{large}{latex}
{tip}This result for the normal force is less than the person's usual weight, in agreement with our expectation that the person should feel lighter while accelerating downward.{tip}
|
| Tip |
|---|
Is it clear why the acceleration must have a minus sign? |
| Tip |
|---|
This result for the normal force is less than the person's usual weight, in agreement with our expectation that the person should feel lighter while accelerating downward. |
|
| Card |
|---|
| unmigrated-wiki-markup |
h2. Part B
Suppose a person with a weight of 686 N is in an elevator which is has been ascending at a constant rate of 1.0 m/s and is now slowing down at a rate of 3.0 m/s {color:black}^2^{color}. What is the 2. What is the person's apparent weight? Solution System, Interactions and Model: Approach: | Cloak |
|---|
|
h4. Solution
*System, Interactions and Model:* As in Part A.
*Approach:* As in Part A, the acceleration is negative in our coordinates. The free body diagram is also the same, and so we find the same result:
{latex}\begin{large}\[ N = \mbox{476 N} \]\end{large}{latex}
| |
|
| Card |
|---|
| unmigrated-wiki-markup |
h2. Part C
Suppose a person with a weight of 686 N is in an elevator which is ascending at a constant rate of 1.0 m/s and speeding up at a rate of ascending, speeding up at a rate of 3.0 m/s {color:black}^2^{color}. What is the 2. What is the person's apparent weight? Solution System, Interactions and Model: Approach:| Cloak |
|---|
|
h4. Solution
*System, Interactions and Model:* As in Part A.
*Approach:* The free body diagram and form of Newton's 2nd Law is the same as in Part A, except that the relative size of the forces will be different. We can see this by writing Newton's 2nd Law for the y-direction:
{latex}\begin{large}\[ N = ma_{y} + mg \]\end{large}{latex}
This time, however, the acceleration is positive (_a_~y~ = + 3.0 m/s{color:black}^2^{color}) giving:
{latex}\begin{large}\[ N = \mbox{896 N} \] \end{large}{latex}
{tip}Upward acceleration increases the perceived weight.{tip}
| |
|
|