...
A
...
4460
...
lb
...
Ford
...
Explorer
...
traveling
...
35
...
mph
...
has
...
a
...
head
...
on
...
collision
...
with
...
a
...
2750
...
lb
...
Toyota
...
Corolla,
...
also
...
traveling
...
35
...
mph.
| Excerpt | ||
|---|---|---|
| ||
Compare the forces on the occupants of two cars in a 1-D totally inelastic collision. |
| Composition Setup |
|---|
| Deck of Cards | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
{excerpt:hidden=true}Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.{excerpt}
{composition-setup}{composition-setup}
{deck:id=bigdeck}
{card:label=Part A}
h2. Part A
Assuming that the automobiles become locked together during the collision, what is the speed of the combined mass immediately after the collision?
h4. Solutions
{toggle-cloak:id=sysa} *System:* {cloak:id=sysa}Explorer plus Corolla as [point particles|point particle].{cloak}
{toggle-cloak:id=inta} *Interactions:* {cloak:id=inta}Impulse resulting from external influences will be neglected, as we assume that the collision is instantaneous.{cloak}
{toggle-cloak:id=moda} *Model:* {cloak:id=moda}[Momentum and External Force].{cloak}
{toggle-cloak:id=appa} *Approach:*
{cloak:id=appa}
{toggle-cloak:id=diaga} {color:red} *Diagrammatic Representation* {color}
{cloak:id=diaga}
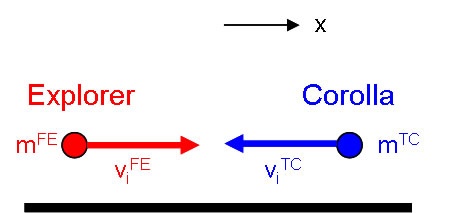
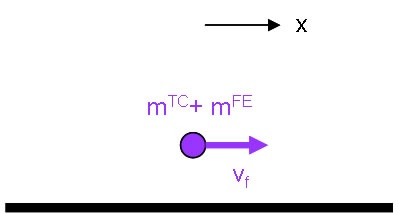
We begin by sketching the situation and defining a coordinate system.
|!CollisionInit.jpg!|!CollisionFin.jpg!|
||Initial State||Final State||
{cloak:diaga}
{toggle-cloak:id=matha} {color:red} *Mathematical Representation* {color}
{cloak:id=matha}
Since we assume that external forces are negligible during the collision, we set the external impulse to zero which gives:
{latex}
|