| Card |
|---|
| | Wiki Markup |
|---|
h3. Part A
A 3.0 m long ladder is leaned against a vertical wall at a 70° angle above the horizontal. The wall is frictionless, but the (level) floor beneath the ladder does have friction. Assuming the center of mass of the 15.0 kg ladder is in its exact center, find the forces exerted on the ladder by the wall and by the floor. Solution System: Interactions: | Cloak |
|---|
| External influences from the earth (gravity) the wall (normal force) and the floor (normal force and frictional force). |
Model: Approach: Diagrammatic RepresentationThis is a statics problem, so the object is to ensure that the ladder does not rotate or translate. Thus, we know that all accelerations and angular accelerations are zero. We first sketch the situation and set up coordinates, which includes selecting an axis. Selecting the position of the axis is technically arbitrary, but often it is actually specified by the unknowns in the system. In this case, as we shall see, the forces in the x-direction are less constrained than the y-direction forces. Thus, it is a good idea to position the axis to cancel the torque from one of the x forces. We choose to put the axis at the point of contact with the floor. 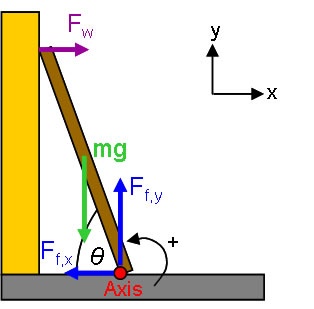 Image Added Image Added
Mathematical Representation We then write the equations of linear and rotational equilibrium: | Latex |
|---|
a 70° angle above the horizontal. The wall is frictionless, but the (level) floor beneath the ladder does have friction. Assuming the center of mass of the 15.0 kg ladder is in its exact center, find the forces exerted on the ladder by the wall and by the floor.
h4. Solution
{toggle-cloak:id=sysa} *System:* {cloak:id=sysa} The ladder as a [rigid body].{cloak}
{toggle-cloak:id=inta} *Interactions:* {cloak:id=inta}External influences from the earth (gravity) the wall (normal force) and the floor (normal force and frictional force).{cloak}
{toggle-cloak:id=moda} *Model:* {cloak:id=moda}[Single-Axis Rotation of a Rigid Body] and [Point Particle Dynamics].{cloak}
{toggle-cloak:id=appa} *Approach:*
{cloak:id=appa}
{toggle-cloak:id=diaga} {color:red} *Diagrammatic Representation*{color}
{cloak:id=diaga}
This is a [statics] problem, so the object is to ensure that the ladder does _not_ rotate or translate. Thus, we know that all accelerations and angular accelerations are zero. We first sketch the situation and set up coordinates, which includes selecting an axis. Selecting the position of the axis is technically arbitrary, but often it is actually specified by the unknowns in the system. In this case, as we shall see, the forces in the x-direction are less constrained than the y-direction forces. Thus, it is a good idea to position the axis to cancel the torque from one of the x forces. We choose to put the axis at the point of contact with the floor.
!ladder1.jpg!
{cloak:diaga}
{toggle-cloak:id=matha} {color:red} *Mathematical Representation* {color}
{cloak:id=matha}
We then write the equations of linear and rotational equilibrium:
{latex}\begin{large}\[ \sum F_{x} = F_{w} + F_{f,x} = 0 \]
\[ \sum F_{y} = - mg + F_{f,y} = 0 \]
\[ \sum \tau = + mg (L/2) \cos\theta - F_{w} L \sin\theta \]\end{large}{latex}
{note}Note that our selection of the axis point guaranteed that the floor's force would contribute zero torque.{note}
The y-direction equation and the torque equation are immediately solvable to obtain:
{latex} |
| Note |
|---|
Note that our selection of the axis point guaranteed that the floor's force would contribute zero torque. |
The y-direction equation and the torque equation are immediately solvable to obtain: | Latex |
|---|
\begin{large} \[ F_{f,y} = mg = \mbox{147 N}\]
\[ F_{w} = \frac{mg}{2}\cot\theta = \mbox{27 N}\]\end{large}{latex}
|
Once we have _F _~w~w, we can find the x-component of the floor's force:
{| Latex |
|---|
}\begin{large}\[ F_{f,x} = -F_{w} = - \mbox{27 N}\]\end{large}{latex}
| We can now construct the total floor force: 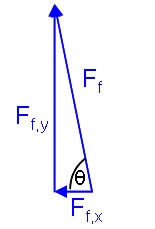 Image Added Image Added
Which gives a total force of 150 N at 80° above the horizontal. | Cloak |
|---|
|
!ladderfloorforce.jpg!
Which gives a total force of 150 N at 80° above the horizontal.
{cloak:matha}
{cloak:appa}
| |
|
| Card |
|---|
| unmigrated-wiki-markup |
h3. Part B
Consider the same basic situation as in Part A, but now suppose that the wall has friction. If the coefficient of static friction between the floor and the ladder is only 0.15, what is the minimum coefficient of static friction needed between the wall and the ladder to prevent the ladder from slipping?
h4. Solution
{Solution:=} *System:* {:=} [rigid body].{cloak}
{:=} *Interactions:* {:=} {cloak}
{:=} * Model: Approach: An Important Assumption The minimum coefficient of friction will occur when both friction forces are maxima. Thus, we have the important relationships: | Latex |
|---|
* {cloak:id=modb}[Single-Axis Rotation of a Rigid Body] and [Point Particle Dynamics].{cloak}
{toggle-cloak:id=appb} *Approach:*
{cloak:id=appb}
{toggle-cloak:id=prelim} {color:red} *An Important Assumption* {color}
{cloak:id=prelim}
The minimum coefficient of friction will occur when both friction forces are maxima. Thus, we have the important relationships:
{latex}\begin{large}\[ |F_{f,x}| = \mu_{s,f} |F_{f,y}| \]
\[ |F_{w,y}| = \mu_{s,w} |F_{w,x}| \]\end{large}{latex}
{cloak:prelim}
{ |
: Diagrammatic Representation Because we know the floor's static friction coefficient, we can streamline the solution by switching our choice of axis.  Image Added Image Added
Mathematical Representation The resulting equations are: | Latex |
|---|
=diagb} {color:red} *Diagrammatic Representation* {color}
{cloak:id=diagb}
Because we know the floor's static friction coefficient, we can streamline the solution by switching our choice of axis.
!ladder2.jpg!
{cloak:diagb}
{toggle-cloak:id=mathb} {color:red} *Mathematical Representation* {color}
{cloak:id=mathb}
The resulting equations are:
{latex}\begin{large}\[ \sum F_{x} = F_{w,x} - \mu_{s,f}F_{f,y} = 0 \]
\[ \sum F_{y} = - mg + F_{f,y} + \mu_{s,w}F_{w,x}= 0 \]
\[ \sum \tau = - mg (L/2) \cos\theta + F_{f,y} L\cos\theta - \mu_{s,f}F_{f,y} L \sin\theta \]\end{large}{latex}
{note}Note that the |
| Note |
|---|
Note that the y-component of the floor force is the normal force from the floor on the ladder, and the x-component of the wall force is the normal force from the wall on the ladder. Since we are assuming static friction is maximized, we have rewritten _F _~ff, x~ x and _F _~ww, y~ y as the coefficient of friction times the relevant normal force. {note}
|
The only equation that can be solved immediately is torque balance, which gives:
{| Latex |
|---|
}\begin{large}\[ F_{f,y} = \frac{mg}{2\left(1-\mu_{s,f}\tan\theta\right)} = \mbox{125 N} \]\end{large}{latex}
| We can then substitute this result into the equation of x-force balance to find:
{| Latex |
|---|
}\begin{large}\[ F_{w,x} = \mu_{s,f}F_{f,y} = \mbox{18.8 N} \]\end{large}{latex}
| Finally, we can find the required coefficient of static friction to be:
{| Latex |
|---|
}\begin{large}\[ \mu_{s,w} = \frac{mg-F_{f,y}}{F_{w,x}} = 1.19 \] \end{large}{latex}
{tip}We found in Part A that the ladder is stable as long as the coefficient of friction with the ground is 0.19 or greater, even if there is no friction at all from the wall. Does it make sense that in Part B the wall's friction coefficient has to be so much larger than 0.19 if the wall is only partly responsible for keeping the ladder from sliding?{tip}
{cloak:mathb}
{cloak:appb}
| | Tip |
|---|
We found in Part A that the ladder is stable as long as the coefficient of friction with the ground is 0.19 or greater, even if there is no friction at all from the wall. Does it make sense that in Part B the wall's friction coefficient has to be so much larger than 0.19 if the wall is only partly responsible for keeping the ladder from sliding? |
|
|