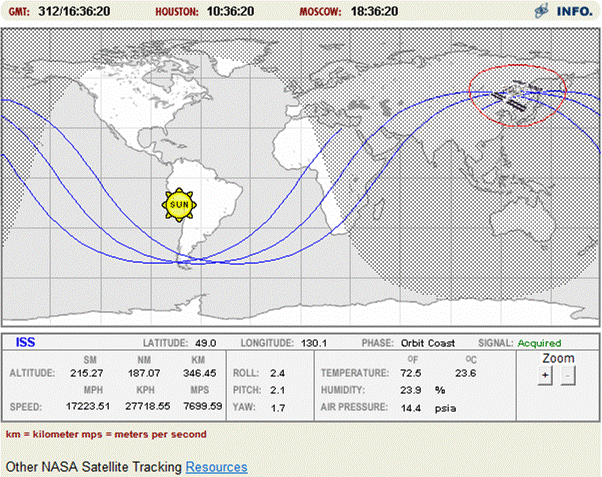
By navigating to the site http://spaceflight.nasa.gov/realdata/tracking/ you can obtain tracking information giving the altitude and speed of the international space stationInternational Space Station (ISS). Suppose that the information displayed on the site was as shown in the screen capture above. By making the assumption that the space station's orbit is a circle with its center at the center of the earth,
| Excerpt |
|---|
find the approximate magnitude of the acceleration experienced by the space station as a result of the gravitational pull of the earth. |
Solution
System: The ISS will be treated as a point particle. Interactions: External influence from the earth (gravity). Model: Uniform Circular Motion. Approach: Based upon the assumption of uniform circular motion, the acceleration of the ISS must satisfy:
| Latex |
|---|
\begin{large}\[ a = \frac{v^{2}}{r} \] \end{large} |
We know that v = 7699.59 m/s, but r requires some thought. The altitude of 346450 m is not the full radius of the orbit, it is only the height of the ISS above the surface of the earth. To find the full orbital radius, we must add on the earth's radius. The earth's radius can be found on the web or in a number of books to be Re = 6,380,000 m. Thus, the orbital radius is r = 6,730,000 m. With this determined, we find:
| Latex |
|---|
\begin{large} \[ a = \mbox{8.81 m/s}^{2} \] \end{large} |
| Note |
|---|
Earth's gravity is not insignificant at level of the ISS's orbit. If it was, the ISS would just fly off into space! |
