Method 1: Angular Momentum| Wiki Markup |
|---|
h4. Method 1
{:=} * System: Interactions: | Cloak |
|---|
| External forces of gravity, normal force and kinetic friction. |
Model: Approach: Diagrammatic RepresentationWe begin with a free body diagram. Since this problem will deal with rotation, we must also select an axis of rotation. 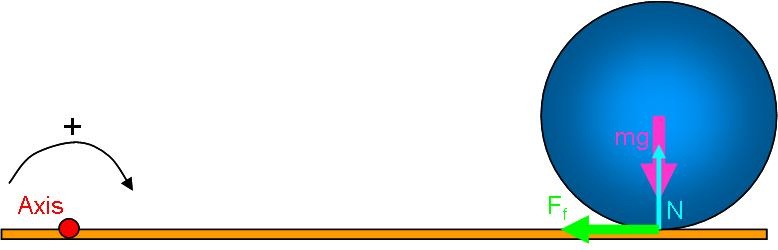 Image Added Image Added
In this case, the most direct (but probably not the most obvious) method of solution is to consider the angular momentum about an axis fixed at some point on the alley surface. For simplicity, we select the point at which the ball is released. By taking a point on the alley surface, we have guaranteed that there is zero net torque acting on the system (the ball) about this axis. Gravity and the normal force each create a nonzero torque, but they balance each other perfectly because they share the same moment arm and they have the same magnitude. The friction force produces no torque because it has zero lever arm.  Image Added Image Added
| Note |
|---|
If it is not apparent to you that the force of gravity and the normal force acting on the ball have equal magnitudes, you should write Newton's 2nd Law for the y-direction. |
Mathematical RepresentationThe angular momentum about a single axis of the ball about the axis we have chosen can be broken into two parts by considering the contribution of the translation of the ball's center of mass and the rotation of the ball about its center of mass. | Latex |
|---|
* {cloak:id=sys1}The ball as a [rigid body].{cloak}
{toggle-cloak:id=int1} *Interactions:* {cloak:id=int1}External forces of gravity, normal force and kinetic friction.{cloak}
{toggle-cloak:id=mod1} *Model:* {cloak:id=mod1}[1-D Angular Momentum and Torque].{cloak}
{toggle-cloak:id=app1} *Approach:*
{cloak:id=app1}
{toggle-cloak:id=diag1} {color:red} *Diagrammatic Representation* {color}
{cloak:id=diag1}
We begin with a free body diagram. Since this problem will deal with rotation, we must also select an axis of rotation.
!bowlballfbd.jpg!
In this case, the most direct (but probably not the most obvious) method of solution is to consider the angular momentum about an axis fixed at some point on the alley surface. For simplicity, we select the point at which the ball is released. By taking a point on the alley surface, we have guaranteed that there is zero net torque acting on the system (the ball) about this axis. Gravity and the normal force each create a nonzero torque, but they balance each other perfectly because they share the same [moment arm] and they have the same magnitude. The friction force produces no torque because it has zero lever arm.
!bowlballleverarm.jpg!
{note}If it is not apparent to you that the force of gravity and the normal force acting on the ball have equal magnitudes, you should write Newton's 2nd Law for the y-direction.{note}
{cloak:diag1}
{toggle-cloak:id=math1} {color:red} *Mathematical Representation* {color}
{cloak:id=math1}
The [angular momentum (one-dimensional)] of the ball about the axis we have chosen can be broken into two parts by considering the contribution of the translation of the ball's center of mass and the rotation of the ball about its center of mass.
{latex}\begin{large}\[ L = L_{\rm trans} + L_{\rm rot} = mvmRv + I\omega \] \end{large}{latex}
|
Since there is zero net torque acting on the ball, the angular momentum is conserved and we can write:
{| Latex |
|---|
}\begin{large}\[ mvmRv_{f} + I\omega_{f} = mvmRv_{i}+I\omega_{i} \] \end{large}{latex}
| We know that ω~i~ = that ωi = 0, and we also know that the ball ends up rolling without slipping. Thus, we know that:
{| Latex |
|---|
}\begin{large}\[ \omega_{f}R = v_{f}\]\end{large}{latex}
| Thus, we have:
{| Latex |
|---|
}\begin{large}\[ v_{f} = \frac{v_{i}}{1+\frac{\displaystyle I}{\displaystyle mR^{2}}} = \frac{v_{i}}{1+\frac{\displaystyle 2}{\displaystyle 5}} = \frac{5}{7} v_{i} = \mbox{2.0 m/s} \]\end{large}{latex}
{cloak:math1}
{cloak:app1}
| |