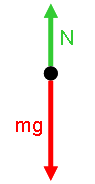| Excerpt |
|---|
|
Finding apparent weight using normal force. |
| Composition Setup |
|---|
cloak.memory.duration = 0
|
One way that we perceive weight is the normal force we experience from the ground. In physics problems, when you are asked to determine apparent weight, the quickest method is usually to compute the normal force provided by the "ground".
...
| Deck of Cards |
|---|
|
| Card |
|---|
| unmigrated-wiki-markup |
h2. Part A
Suppose a person with a weight of 686 N is in an elevator which is descending accelerating downwards at a constant rate of 1.0 m/s and speeding up at a rate of 3.0 m/s {color:black}^2^{color}. What is the 2. What is the person's apparent weight?
h4. Solution
{Solution:=} * System: Interactions: | Cloak |
|---|
| External influences from the earth (gravity) and the floor of the elevator (normal force). |
Model: Approach: Diagrammatic RepresentationsThe physical picture and free body diagram for the person is: 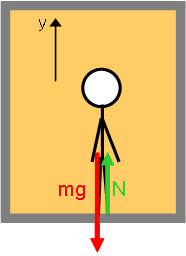 Image Added Image Added | 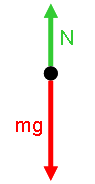 Image Added Image Added | Physical Picture | Free Body Diagram |
|---|
which leads to the form of Newton's 2nd Law for the y direction: | Latex |
|---|
* {cloak:id=Asys}Person as a [point particle].{cloak}
{toggle-cloak:id=Aint} *Interactions:* {cloak:id=Aint}External influences from the earth (gravity) and the floor of the elevator (normal force).{cloak}
{toggle-cloak:id=Amod} *Model:* {cloak:id=Amod}[Point Particle Dynamics].{cloak}
{toggle-cloak:id=Aapp} *Approach:*
{cloak:id=Aapp}
{toggle-cloak:id=AFBD} *Diagrammatic Representations*
{cloak:id=AFBD}The physical picture and free body diagram for the person is:
|!elevator1.gif!|!elevator2.gif!|
||Physical Picture||Free Body Diagram||
{cloak:AFBD}
{toggle-cloak:id=Amath} *Mathematical Representation*
{cloak:id=Amath}which leads to the form of [Newton's 2nd Law|Newton's Second Law] for the _y_ direction:
{latex}\begin{large}\[ \sum F_{y} = N - mg = ma_{y} \]\end{large}{latex}
|
In our coordinates, the acceleration of the person is _a _~y~ y = -3.0 m/s2, giving: | Latex |
|---|
{color:black}^2^{color}, giving:
{latex}\begin{large}\[ N = ma_{y} + mg = \mbox{476 N} \]\end{large}{latex}
{cloak:Amath}
{toggle-cloak:id=Acheck} *Is the answer sensible?*
{cloak:id=Acheck}
{tip}This result for the normal force is less than the person's usual weight, in agreement with our expectation that the person should feel lighter while accelerating downward.{tip}
{cloak:Acheck}
{cloak:Aapp}
|
| Tip |
|---|
Is it clear why the acceleration must have a minus sign? |
| Tip |
|---|
This result for the normal force is less than the person's usual weight, in agreement with our expectation that the person should feel lighter while accelerating downward. |
|
| Card |
|---|
| Part BSuppose a person with a weight of 686 N is in an elevator which is has been ascending at a constant rate of 1.0 m/s and is now slowing down at a rate of 3.0 m/s2. What is the person's apparent weight? Solution System, Interactions and Model: Approach: |
| Card |
|---|
| Part CSuppose a person with a weight of 686 N is in an elevator which is ascending at a constant rate of 1.0 m/s and , speeding up at a rate of 3.0 m/s2. What is the person's apparent weight? Solution System, Interactions and Model: Approach: |
|