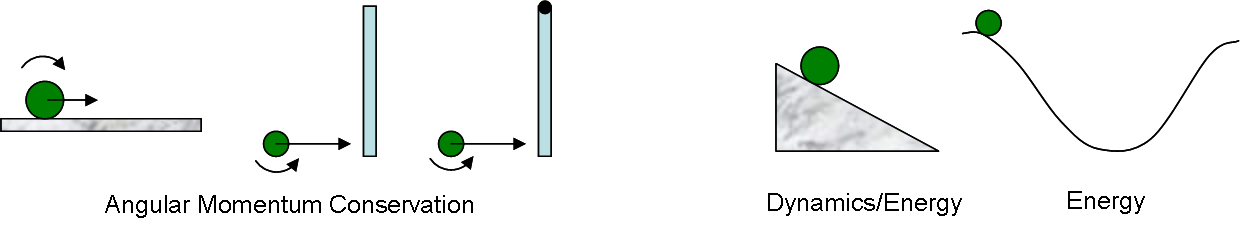...
Many
...
students
...
have
...
asked
...
about
...
when
...
to
...
include
...
center
...
of
...
mass
...
motion
...
when
...
calculating
...
angular
...
momentum
...
and
...
energy.
...
In
...
this
...
page,
...
we
...
give
...
a
...
discussion
...
of
...
some
...
of
...
the
...
main
...
issues.
...
Issue
...
1:
...
Pure
...
Rotation
...
and
...
the
...
Parallel
...
Axis
...
Theorem
...
Recognizing
...
Pure
...
Rotation
...
One
...
key
...
idea
...
in
...
determining
...
how
...
to
...
describe
...
rotational
...
problems
...
is
...
recognizing
...
whether
...
the
...
problem
...
can
...
be
...
treated
...
as
...
pure
...
rotation.
...
Whenever
...
an
...
object
...
is
...
spinning
...
around
...
a
...
fixed
...
axle,
...
we
...
can
...
choose
...
to
...
describe
...
that
...
motion
...
as
...
pure
...
rotation
...
about
...
the
...
axle,
...
even
...
if
...
the
...
center
...
of
...
mass
...
is
...
not
...
located
...
at
...
the
...
axle.
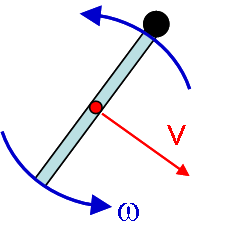
Two Descriptions of Pure Rotation: The Parallel Axis Theorem vs. Rotation and Translation
An object moving in pure rotation about an axle can be described in two different but equivalent ways.
- The object is only rotating, but the moment of inertia about the fixed axle must be found using the parallel axis theorem.
- The object is rotating about the center of mass and its center of mass is translating.
To see why these descriptions are equivalent, consider how we would find the angular momentum and kinetic energy of a bar pivoted at one end.
...
Method 1: The bar is purely rotating. We do not include any contribution from the CM motion.
...
| Latex |
|---|
*. h5. Two Descriptions of Pure Rotation: The Parallel Axis Theorem vs. Rotation and Translation An object moving in pure rotation about an axle can be described in *two different but equivalent ways*. # The object is *only rotating*, but the moment of inertia about the fixed axle must be found using the parallel axis theorem. # The object is *rotating about the center of mass and its center of mass is translating*. To see why these descriptions are equivalent, consider how we would find the angular momentum and kinetic energy of a bar pivoted at one end. h6. Method 1: The bar is purely rotating. We do not include any contribution from the CM motion. !CalcRotRod1.png|width=125px! {latex}\begin{large}\[ L = I\omega = \frac{1}{3}mL^{2}\omega \qquad\qquad\qquad K = \frac{1}{2}I\omega^{2} = \frac{1}{6}mL^{2}\omega^{2}\]\end{large}{latex} h6. Method |
Method 2:
...
The
...
bar
...
is
...
rotating
...
about
...
its
...
CM
...
and
...
the
...
CM
...
is
...
translating.
| Latex |
|---|
!CalcRotRod2.png|width=150px! {latex}\begin{large}\[ L = \vec{r}\times m\vec{v}_{CM} + I_{CM}\omega = \frac{L}{2}mv_{CM} + \frac{1}{12}mL^{2}\omega \qquad\qquad\qquad K = \frac{1}{2}mv_{CM}^{2} + \frac{1}{2}I_{CM}\omega^{2} \]\end{large}{latex} |
To
...
see
...
that
...
Method
...
2
...
is
...
equivalent
...
to
...
Method
...
1,
...
we
...
must
...
realize
...
that
...
the
...
center
...
of
...
mass
...
speed
...
is
...
related
...
to
...
the
...
rotational
...
velocity
...
of
...
the
...
bar
...
by
...
the
...
distance
...
of
...
the
...
CM
...
from
...
the
...
axis
...
of
...
rotation:
| Latex |
|---|
}\begin{large}\[ \omega \frac{L}{2} = v_{CM} \]\end{large}{latex} |
You
...
can
...
now
...
substitute
...
this
...
into
...
the
...
expressions
...
for
...
L
...
and
...
K:
| Latex |
|---|
}\begin{large}\[ L = \left(\frac{L}{2}\right)^{2} m\omega + \frac{1}{12}mL^{2} \omega = \frac{1}{3}mL^{2}\omega \qquad\qquad\qquad K = \frac{1}{2}m\left(\frac{L}{2}\right)^{2} \omega^{2} + \frac{1}{2}\left(\frac{1}{12}\right)mL^{2}\omega^{2} = \frac{1}{6}mL^{2}\omega^{2}\]\end{large}{latex} |
which
...
are
...
equivalent
...
to
...
the
...
expressions
...
found
...
in
...
Method
...
1.
...
Parallel
...
Axis
...
Theorem
...
and
...
Dynamics
...
Generally
...
it
...
is
...
advantageous
...
use
...
the
...
parallel
...
axis
...
theorem
...
and
...
consider
...
the
...
motion
...
to
...
be
...
pure
...
rotation.
...
The
...
problem
...
of
...
the
...
rod
...
pivoted
...
about
...
one
...
end
...
is
...
a
...
good
...
example
...
of
...
why.
...
If
...
you
...
are
...
asked
...
to
...
find
...
the
...
angular
...
acceleration
...
of
...
the
...
rod
...
or
...
to
...
find
...
the
...
frequency
...
of
...
small
...
oscillations,
...
you
...
will
...
need
...
to
...
compute
...
the
...
torque
...
around
...
the
...
pivot
...
and
...
set
...
that
...
torque
...
equal
...
to
...
I
...
times alpha
...
.
...
The
...
appropriate
...
moment
...
of
...
inertia
...
to
...
use
...
is
...
the
...
moment
...
of
...
inertia
...
about
...
the
...
end
...
of
...
the
...
rod.
...
...
Issue 2:
...
Rotation
...
plus
...
Translation
...
and
...
External
...
or
...
CM
...
Axis
...
Dynamics,
...
Energy
...
Conservation,
...
or
...
Angular
...
Momentum
...
Conservation?
...
When
...
deciding
...
how
...
to
...
deal
...
with
...
an
...
object
...
that
...
cannot
...
be
...
considered
...
to
...
be
...
purely
...
rotating,
...
you
...
must
...
first
...
decide
...
whether
...
you
...
will
...
be
...
using
...
angular
...
momentum
...
conservation.
...
We
...
know
...
two
...
basic
...
situations
...
that
...
are
...
often
...
treated
...
with
...
angular
...
momentum
...
conservation
...
and
...
can
...
involve
...
a
...
rotating
...
and
...
translating
...
object:
...
- Collisions
...
- that
...
- result
...
- in
...
- rotation.
...
- Bowling
...
- balls
...
- or
...
- other
...
- objects
...
- rolling
...
- and
...
- slipping
...
- on
...
- a
...
- level
...
- surface.
...
Other
...
situations
...
must
...
generally
...
be
...
dealt
...
with
...
using
...
dynamics
...
or
...
energy
...
conservation.
...
The
...
most
...
common
...
example
...
is
...
an
...
object
...
rolling
...
on
...
a
...
ramp
...
or
...
track.
Angular Momentum Conservation requires Stationary Axis
Problems involving conservation of angular momentum essentially require that you choose a stationary axis that lies outside the objects involved. For the bowling ball, the axis must lie on the ground (see Down the Alley). For a collision, the axis is generally placed either at the fixed axis of the collision target (if it is attached to a pivot), at the level of the system CM for a free target that sticks to the incoming object, and at the level of the target CM for a free target that does not stick to the incoming object.
The angular momentum of a rotating and translating object about a stationary external axis is given by:
| Latex |
|---|
!CalcRotBall1.png|width=900px! h5. Angular Momentum Conservation requires Stationary Axis Problems involving conservation of angular momentum essentially require that you choose a stationary axis that lies outside the objects involved. For the bowling ball, the axis must lie on the ground (see [Down the Alley]). For a collision, the axis is generally placed either at the fixed axis of the collision target (if it is attached to a pivot), at the level of the system CM for a free target that sticks to the incoming object, and at the level of the target CM for a free target that does not stick to the incoming object. The angular momentum of a rotating and translating object about a stationary external axis is given by: {latex}\begin{large}\[ L = \vec{r}\times m\vec{v}_{CM} + I_{CM} \omega \]\end{large}{latex} h5. Dynamics or Conservation of Energy requires CM Axis Problems involving dynamics or conservation of energy of an object rolling along a ramp or track are most easily solved by placing the axis of rotation at the object's center of mass. The translation of the center of mass and the rotation about the center of mass must then be considered separately. For dynamics, the translation will be governed by F = ma and the rotation will be governed by τ = I{~}CM{~}α. For energy, the kinetic energy of the object will be: {latex} |
Dynamics or Conservation of Energy requires CM Axis
Problems involving dynamics or conservation of energy of an object rolling along a ramp or track are most easily solved by placing the axis of rotation at the object's center of mass. The translation of the center of mass and the rotation about the center of mass must then be considered separately. For dynamics, the translation will be governed by F = ma and the rotation will be governed by torque equals ICM times alpha. For energy, the kinetic energy of the object will be:
| Latex |
|---|
\begin{large}\[ K = \frac{1}{2}mv_{CM}^{2} + \frac{1}{2}I_{CM}\omega^{2}\]\end{large}{latex}
Note that if the object is rolling without slipping, the speed of the CM and the angular velocity of the rotation about the CM can be related by using the radius of the object.
|
Note that if the object is rolling without slipping, the speed of the CM and the angular velocity of the rotation about the CM can be related by using the radius of the object.
...
Issue 3: Orbits
Background: Point Masses
Satellites in orbit are an excellent example of the point mass approximation. Their size and rotation are completely negligible when compared to the radius of the orbit and their orbital speed. Point masses have zero ICM. Thus, they never have two parts to their angular momentum or kinetic energy.
You can choose to write their angular momentum as:
| Latex |
|---|
\begin{large}\[ L = I\omega \]\end{large} |
or
| Latex |
|---|
\begin{large}\[L = \vec{r}\times m\vec{v} = rmv_{\perp}\]\end{large} |
where the last expression contains the part of v that is perpendicular to the radial line from the axis of rotation (the center of the planet for orbits).
These two expressions for the angular momentum are totally equivalent, because for a point mass
| Latex |
|---|
\begin{large}\[I = mr^{2}\]\end{large} |
and
| Latex |
|---|
\begin{large}\[ r\omega = v_{\perp} \]\end{large} |
. Substituting these into the first equation for L will give the second equation.
The kinetic energy should simply be written as:
| Latex |
|---|
\begin{large}\[ K = \frac{1}{2} mv^{2} \]\end{large} |
because the entire velocity contributes to the kinetic energy, not just the part perpendicular to the radial line. In a perfectly circular orbit (where the whole velocity is perpendicular to the radius), one-half m v squared is equivalent to one-half I omega squared, but in an elliptical orbit it is not.
Special Points: Extrema
The min and max distance from the planet in an elliptical orbit are special, because they are the only places that the velocity is exactly perpendicular to the radial line. Thus, the angular momentum at these extrema is easy:
| Latex |
|---|
\begin{large}\[ L_{ex} = mr_{ex}v_{ex} \]\end{large} |
| Wiki Markup |
|---|
{html}
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>
{html} |