Versions Compared

Old Version 43

changes.mady.by.user Analia Barrantes

Saved on

compared with

New Version Current

changes.mady.by.user Analia Barrantes

Saved on

Key

  • This line was added.
  • This line was removed.
  • Formatting was changed.
Comment: Migration of unmigrated content due to installation of a new plugin
unmigratedcomposition-wiki-markupsetup
A 
...
 uniform 
...
 bar 
...
 of 
...
 mass 
...
M
...
 and 
...
 length 
...
d
...
 is 
...
 initially 
...
 at 
...
 rest 
...
 on 
...
 a 
...
 horizontal 
...
 and 
...
 frictionless 
...
 table. 
...
 A 
...
 ball 
...
 of 
...
 mass 
...
m
...
 and 
...
 very 
...
 small 
...
 radius 
...
 is 
...
 moving 
...
 towards 
...
 the 
...
 bar 
...
 with 
...
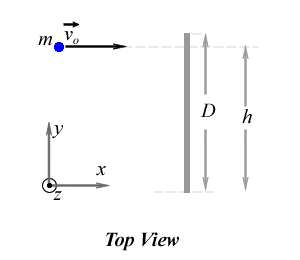
 speed vo, hits and sticks to the bar at a distance h measured from on end of the bar. The bar is not attached to the table and its moment of inertia with respect to its center of mass is known to be Icm. The goal of the problem is to 
 Excerpt
find the angular velocity and the velocity of the final object's (bar + ball) center of mass
.
 Center
 Image Added
Solution
 Toggle Cloak
idsys
 System: 
 Cloak
idsys
The ball is treated as a point mass and the bar as a rigid body with its mass uniformly distributed. 
 Cloak
sys
sys
 Toggle Cloak
idint
 Interactions: 
 Cloak
idint
 The system experiences external interactions from the earth (gravity) and the table's surface (only normal force because the surface is frictionless). Since gravity and the normal force are both purely vertical forces in this problem, there are no external horizontal forces. For the same reason, there is no external torque about any vertical axis of rotation.
 Cloak
int
int
 Toggle Cloak
idmod
 Models: 
 Cloak
idmod
Angular Momentum and External Torque about a Single Axis and Momentum and External Force.
 Cloak
mod
mod

 Toggle Cloak
idapp
 Approach:
 Cloak
idapp
 Toggle Cloak
idcons
 Consider the Motion
 Cloak
idcons
The motion of the objects before and after the collision is on the table's surface, (x,y) plane. The coordinate system used in this problem is shown in the figure above. After the collision, the ball-bar system will translate to the right and rotate counter-clockwise about its center of mass which is not at the center of the bar but at some point between the ball and the center of the bar.  
 Because the rigid body translates and rotates we will apply linear momentum and impulse and angular momentum and angular impulse principles to the ball-bar system. For that purpose we need to calculate the sum of the external forces exerted on the system as well as the sum of the torques due to the external forces about a given point. 

 Cloak
cons
cons
 Toggle Cloak
idsumforce
 The Net External Force
 Cloak
idsumforce
The external forces exerted on the system are the gravitational and the normal forces applied at the center of mass of the ball and the bar. Because there is no motion in the direction perpendicular to the table's surface (z-axis) the normal forces on both objects have the same magnitude but opposite direction than the respective gravitational forces. Therefore, the sum of the external forces on the system is zero and the linear momentum of the system is constant:
 Latex
 _v{_}{~}o~, hits and sticks to the bar at a distance _h_ measured from on end of the bar. The bar is not attached to the table and its moment of inertia with respect to its center of mass is known to be _I{_}{~}cm~. The goal of the problem is to find the angular velocity and the velocity of the bar's center of mass.{table:align=center}{tr}{td} !ballBarInelastic.png! {td}{tr}{table}

*{+}Solution{+}{*}*:*
{toc:indent = 10 px}



h2. System: 

The ball is treated as a [point mass|point particle] and the bar as a rigid body with its mass uniformly distributed. The external forces on the system are the result of the interactions between the elements of the system and the Earth (gravitational force on ball and on bar) and with the table's surface (as there is no fricition it is the normal force exerted by the surface on the ball and on the bar).

h2. Model: 
[1-D Angular Momentum and Angular Impulse] and [Momentum and Impulse].

\\
h2. Approach:
The motion of the objects before and after the collision is on the table's surface, _(x,y)_ plane. The coordinate system used in this problem is shown in the figure above.  After the collision, the ball-bar system will translate to the right and rotate counter-clockwise about its center of mass which is not at the center of the bar but at some point between the ball and the center of the bar. 
\\
Because the rigid body translates and rotates we will apply [linear momentum and impulse|Momentum and Impulse] and [angular momentum and angular impulse|1-D Angular Momentum and Angular Impulse] principles to the ball-bar system. For that purpose we need to calculate the sum of the external forces exerted on the system as well as the sum of the torques due to the external forces about a given point.
\\
\\
h4. The sum of the external forces:

The external forces exerted on the system are the gravitational and the normal forces applied at the center of mass of the ball and the bar. Because there is no motion in the direction perpendicular to the table's surface (z-axis) the normal forces on both objects have the same magnitude but opposite direction than the respective gravitational forces. Therefore, the sum of the external forces on the system is zero and the linear momentum of the system is constant:

{latex}\begin{large}$\vec{P}^{before} = \vec{P}^{after}$ \end{large}{latex}



h4. The sum of the external torques about a given point Q:

The net torque due to the external forces about a given point Q is given by:
{latex}
 Cloak
sumforce
sumforce
 Toggle Cloak
idsumtorque
 The Net External Torque
 Cloak
idsumtorque
The net torque due to the external forces about a given point Q is given by:
 Latex
\begin{large} $\sum \tau_{Q}^{ext} = \tau_{Q}^{mg} +\tau_{Q}^{N_{ball}} + \tau_{Q}^{Mg} +\tau_{Q}^{N_{bar}}$ \end{large}{latex}

where 
...
 the 
...
 superscripts 
...
mg
...
 and 
...
Mg
...
 indicate 
...
 the 
...
 torques 
...
 due 
...
 to 
...
 the 
...
 gravitational 
...
 force 
...
 on 
...
 the 
...
 ball 
...
 and 
...
 the 
...
 bar, 
...
 respectively, 
...
 and 
...
 the 
...
 superscripts 
...
N
...
ball
...
 and 
...
N
...
bar
...
 the 
...
 torques 
...
 due 
...
 to 
...
 the 
...
 normal 
...
 force 
...
 on 
...
 the 
...
 ball 
...
 and 
...
 bar, 
...
 respectively.
...
We 
...
 start 
...
 by 
...
 calculating 
...
 the 
...
 torques 
...
 exerted 
...
 on 
...
 the 
...
 ball. 
...
 We 
...
 choose 
...
 an 
...
 arbitratry 
...
 point 
...
Q
...
 on 
...
 the 
...
 table 
...
 and 
...
 we 
...
 measure 
...
 the 
...
 position 
...
 of 
...
 the 
...
 ball's 
...
 center 
...
 of 
...
 mass 
...
 with 
...
 the 
...
 vector 
...
 of 
...
 magnitude 
...
r
...
, 
...
 the 
...
 red 
...
 arrow 
...
 in 
...
 the 
...
 figure. 
...
 The 
...
 black 
...
 arrows 
...
 are 
...
 the 
...
 normal 
...
 force 
...
 and 
...
 the 
...
 gravitational 
...
 force 
...
 exerted 
...
 on 
...
 the 
...
 ball 
...
 of 
...
 magnitudes 
...
N
...
ball
...
 and 
...
F
...
E 
...
 on 
...
 ball
...
, 
...
 respectively. 
...
 Because 
...
 these 
...
 two 
...
 forces 
...
 are 
...
 applied 
...
 at 
...
 the 
...
 same 
...
 point, 
...
 the 
...
 ball's 
...
 center 
...
 of 
...
 mass, 
...
 the 
...
 corresponding 
...
moment 
...
 arms
...
 are 
...
 the 
...
 same. 
...
 In 
...
 addition, 
...
 these 
...
 forces 
...
 have 
...
 the 
...
 same 
...
 magnitude 
...
 but 
...
 opposite 
...
 direction, 
...
 therefore 
...
 the 
...
 torques 
...
 due 
...
 to 
...
 each 
...
 of 
...
 them 
...
 also 
...
 have 
...
 the 
...
 same 
...
 magnitude 
...
 and 
...
 opposite 
...
 direction 
...
 and 
...
 they 
...
 add 
...
 to 
...
 zero. 
...
 The 
...
 torques 
...
 are 
...
 indicated 
...
 with 
...
 the 
...
 purple 
...
 vectors 
...
 in 
...
 the 
...
 figure 
...
 below.
 Center
 Image Added
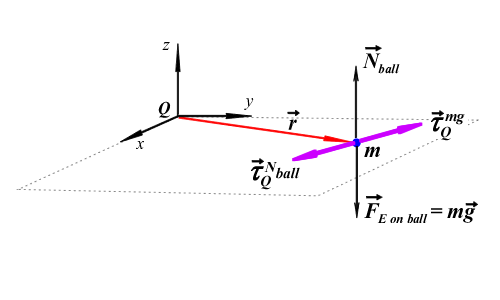
In the same way, we can calculate the torques due to the normal and the gravitational force exerted on the bar. These two forces are also applied at the same point, the centre of mass of the bar, therefore the moment arm about point Q is the same and because these two forces have the same magnitude but opposite direction the resulting torques about point Q will add to zero. We conclude that the sum of the torques due to the external forces on the system about point Q is zero, therefore that angular momentum of the ball-bar system about point Q is constant.
 Latex
{table:align=center}{tr}{td} !FreBodyBall.png! {td}{tr}{table}


In the same way, we can calculate the torques due to the normal and the gravitational force exerted on the bar. These two forces are also applied at the same point, the centre of mass of the bar, therefore the moment arm about point Q is the same and because these two forces have the same magnitude but opposite direction the resulting torques about point Q will add to zero. We conclude that the sum of the torques due to the external forces on the system about point Q is zero, therefore that angular momentum of the ball-bar system about point Q is constant.
{latex}\begin{large} $ \vec {L}_{Q}^{before} =\vec L_{Q}$\end{large} {latex}

{note:title=Note: You can show that in this particular problem the net torque is zero about any point Q in space (not necessarily a point in the plane of the table). As a result, the angular momentum of the ball - bar system is constant about any point in space.
}

{note}
\\

h4. Apply linear momentum and Impulse (Obtain _v{~}cm{~}_):

Before the collision only the ball is moving then the linear momentum of the system is the linear momentum of a point particle of mass _m_ moving with speed _v{~}o{~}_ in the +x-direction:
{latex}
 Note
titleNote
 You can show that in this particular problem the net torque is zero about any point Q in space (not necessarily a point in the plane of the table). As a result, the angular momentum of the ball - bar system is constant about any point in space.

 Cloak
sumtorque
sumtorque
 Toggle Cloak
idlinmom
 Apply the Momentum and External Force Model
 Cloak
idlinmom
Before the collision only the ball is moving then the linear momentum of the system is the linear momentum of a point particle of mass m moving with speed vo in the +x-direction:
 Latex
\begin{large} $\vec P^{before} = m v\hat{x}$\end{large}{latex}

After 
...
 the 
...
 collision 
...
 the 
...
 ball 
...
 stays 
...
 attached 
...
 to 
...
 the 
...
 bar 
...
 and 
...
 they 
...
 are 
...
 both 
...
 translating 
...
 with 
...
 the 
...
 same 
...
 velocity, 
...
 the 
...
 velocity 
...
 of 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 of 
...
 the 
...
 system:

{
 Latex
}\begin{large} $\vec{P}^{after} = (m+M)\vec{v}_{cm}$\end{large}{latex}

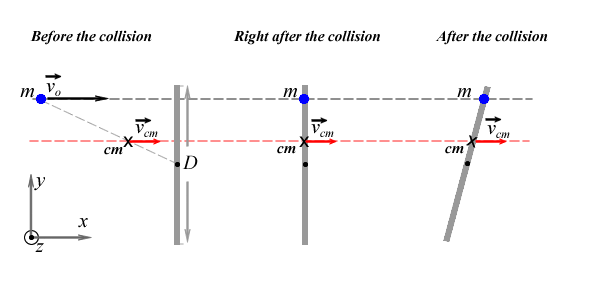
Because 
...
 the 
...
 sum 
...
 of 
...
 the 
...
 external 
...
 forces 
...
 exerted 
...
 on 
...
 the 
...
 system 
...
 is 
...
 zero 
...
 the 
...
 linear 
...
 momentum 
...
 is 
...
 constant. 
...
 Using 
...
 the 
...
 above 
...
 expressions 
...
 we 
...
 obtain 
...
 that 
...
 the 
...
 velocity 
...
 of 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 is:

{
 Latex
}\begin{large}$\vec{v}_{cm} =\frac{mv_o}{m+M}\hat{x}$\end{large}(eq. 1){latex}


Also, 
...
 because 
...
 the 
...
 sum 
...
 of 
...
 the 
...
 external 
...
 forces 
...
 is 
...
 zere 
...
 the 
...
 acceleration 
...
 of 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 is 
...
 zero, 
...
 therefore 
...
 the 
...
 velocity 
...
 of 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 is 
...
 constant 
...
 and 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 of 
...
 the 
...
 system 
...
 moves 
...
 along 
...
 a 
...
 stratight 
...
 line 
...
 (the 
...
 x-component 
...
 of 
...
 the 
...
 position 
...
 of 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 increases 
...
 linearly 
...
 with 
...
 time). 
...
 In 
...
 the 
...
 figure 
...
 below 
...
 the 
...
 motion 
...
 of 
...
 the 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 of 
...
 the 
...
 ball-bar 
...
 system 
...
 is 
...
 hown. 
...
 The 
...
 center 
...
 of 
...
 mass 
...
 is 
...
 indicated 
...
 with 
...
 the 
...
 black 
...
 X 
...
 and 
...
 its 
...
 path 
...
 with 
...
 a 
...
 red 
...
 dotted 
...
 line. 
...
 The 
...
 centre 
...
 of 
...
 mass 
...
 is 
...
 a 
...
 point 
...
 somewhere 
...
 between 
...
 the 
...
 ball 
...
 and 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 of 
...
 the 
...
 bar. 
...
 Note 
...
 that 
...
 only 
...
 after 
...
 the 
...
 collision 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 is 
...
 physically 
...
 located 
...
 inside 
...
 the 
...
 bar.
 Center
 Image Added
 Cloak
linmom
linmom
 Toggle Cloak
idangmom
 Apply the Angular Momentum and External Torque Model
 Cloak
idangmom
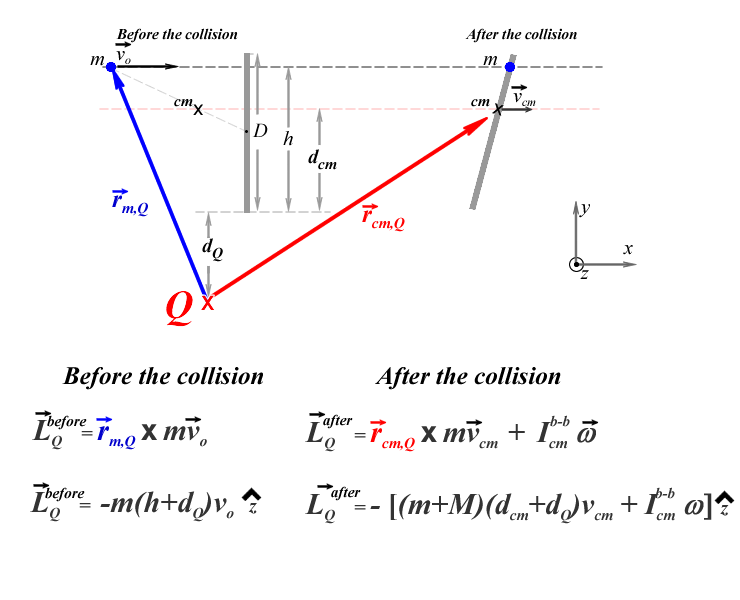
Because the net torque is zero about any point in space we have the freedom to choose it anywhere we want. Let's consider the point Q to be at some point below the lower end of the bar, at a perpendicular distance dQ from the bottom end as shown in red in the figure below.
 Center
 Image Added
The distance between the bottom end of the bar and the straight dotted red line along which the center of mass of the system moves is defined as dcm and is given by:
 Latex
 
{table:align=center}{tr}{td} !BallBarInelastic2.png|width=600,height=300! {td}{tr}{table}


h4. Apply angular momentum and Angular Impulse. (Obtain _w_):

Because the net torque is zero about any point in space we have the freedom to choose it anywhere we want. Let's consider the point Q to be at some point below the lower end of the bar, at a perpendicular distance _d{~}Q{~}_ from the bottom end as shown in red in the figure below.  {table:align=center}{tr}{td} !BallBarInelasticQ.png|width=600,height=600! {td}{tr}{table}

The distance between the bottom end of the bar and the straight dotted red line along which the center of mass of the system moves is defined as _d{~}cm{~}_ and is given by:
{latex}\begin{large}$d_{cm}=\frac{mh+MD/2}{m+M}$\end{large}{latex} 

Before the collision only the ball is moving, therefore the angular momentum of the system is the [angular momentum of a point particle moving along a straight line]. The blue arrow in the figure of magnitude _r{~}m,Q{~}_ is the position vector of the ball measured from point Q before the collision, so the angular momentum about point Q is given by:

{latex}
Before the collision only the ball is moving, therefore the angular momentum of the system is the angular momentum of a point particle moving along a straight line. The blue arrow in the figure of magnitude rm,Q is the position vector of the ball measured from point Q before the collision, so the angular momentum about point Q is given by:
 Latex
\begin{large} $\vec L_{Q}^{before}=\vec{r}_{m,Q} $ x $m\vec{v}_{o} =  -m (h+d_Q)v_o\hat{z}$\end{large} (eq. 2) {latex}

where _
where h+d
...
Q
...
 is 
...
 the 
...
 distance 
...
 between 
...
 point 
...
 Q 
...
 and 
...
 the 
...
 straight 
...
 line 
...
 along 
...
 which 
...
 the 
...
 ball 
...
 moves.
...
After 
...
 the 
...
 collision 
...
 both 
...
 objects 
...
 are 
...
 rotating 
...
 and 
...
 translating 
...
 as 
...
 a 
...
rigid 
...
 body
...
 (the 
...
 ball 
...
 is 
...
 attached 
...
 to 
...
 the 
...
 bar), 
...
 therefore 
...
 the 
...
 angular 
...
 momentum 
...
 of 
...
 the 
...
 ball-bar 
...
 system 
...
 about 
...
 point 
...
 Q 
...
 is 
...
 the 
...
 angular 
...
 momentum 
...
 of 
...
 a 
...
 rigid 
...
 body 
...
 rotating 
...
 clockwise 
...
 with 
...
 angular 
...
 speed 
...
ω and 
...
 translating 
...
 to 
...
 the 
...
 right with speed vcm. The position vector of the center of mass of the system measured from point Q after the collision has magnitude rcm,Q and is indicated in red in the figure, then the angular momentum of the system about point Q is given by:
 Latex
 with speed *{_}v{~}cm{~}{_}*. The position vector of the center of mass of the system measured from point Q after the collision has magnitude _r{~}cm,Q{~}_ and is indicated in red in the figure, then the angular momentum of the system about point Q is given by:

{latex}\begin{large}$\vec L_{Q}^{after} = \vec{r}_{cm,Q} x (m+M)\vec{v}_{cm} + I_{cm}^{b-b}\vec \omega$\end{large}  (eq. 3){latex}

where _I{~}cm{~}{^}
where Icmb-b
...
 is 
...
 the 
...
 moment 
...
 of 
...
 inertia 
...
 of 
...
 the 
...
 ball-bar 
...
 system 
...
 measured 
...
 from 
...
 the 
...
 center 
...
 of 
...
 mass 
...
 of 
...
 the 
...
 system 
...
 and 
...
 is 
...
 given 
...
 by:

{
 Latex
}\begin{large} $I_{cm}^{b-b} = I^{bar} + M(d_{cm}-D/2)^2 + m(h-d_{cm})$^2$\end{large} (eq. 4) {latex}

where _I{^}bar{^} = MD{^}2{^}/12_ is the moment of inertia of the bar about its center of mass. To obtain (eq. 4) we used the [pararell axis theorem]. Both terms in (eq. 3) are vectors pointing in the -z-direction (into the paper) and can the translational part of the angular momentum can be expressed in terms of the distance between point Q and the straight line along which the center of mass is moving: :

{latex
where Ibar = MD2/12 is the moment of inertia of the bar about its center of mass. To obtain (eq. 4) we used the parallel axis theorem. Both terms in (eq. 3) are vectors pointing in the -z-direction (into the paper) and can the translational part of the angular momentum can be expressed in terms of the distance between point Q and the straight line along which the center of mass is moving: :
 Latex
}\begin{large}$\vec L_{Q}^{after} = - ( (m+M)(d_{cm}+d_{Q})v_{cm} + I_{cm}^{b-b}\omega )\hat{z}$\end{large}  (eq. 5){latex}


The angular momentum about point Q before and after the collision are equal, therefore setting 
The angular momentum about point Q before and after the collision are equal, therefore setting (eq.3) 
...
 and 
...
 (eq.5) 
...
 equal 
...
 and 
...
 with 
...
 the 
...
 help 
...
 of 
...
 (eq.1) 
...
 we 
...
 obtain 
...
 that 
...
 the 
...
 angular 
...
 velocity 
...
 is 
...
 given 
...
 by:
 Latex


{latex}$\begin{large} $\omega = \frac{mv_{o}(h-d{cm})}{I_{cm}^{b-b}}$ \end{large}$ (eq. 6){latex}


{note:title=1. Note that the answer does not depend on the choice of point Q. Check it! Choose the point Q at the center of mass of the ball-bar system or a point somewhere in the along which the ball is initially moving and you will obtain the same result as in (eq. 6)}

{note:title=2. Note that the angular velocity is zero when h=d~cm~. Does it make sense? When does this happen?}



 Cloak
angmom
angmom
 Toggle Cloak
idcheck
 Check your Answer
 Cloak
idcheck
 Tip
title1.
 Note that the answer does not depend on the choice of point Q. Check it! Choose the point Q at the center of mass of the ball-bar system or a point somewhere in the along which the ball is initially moving and you will obtain the same result as in (eq. 6)
 Tip
title2.
 Note that the angular velocity is zero when h = dcm. Does it make sense? When does this happen?
 Cloak
check
check
 Cloak
app
app
 Wiki Markup
{html}
<MCE:SCRIPT type="mce-text/javascript"><#comment><#comment></#comment></MCE:SCRIPT>
<MCE:SCRIPT type="mce-text/javascript"><#comment><#comment></#comment></MCE:SCRIPT>
{html}