Part D Image Added Image Added
A person pushes a 10 kg box along a smooth floor by applying force of 20 N. The force is applied at 30° below the horizontal. What is the magnitude of the normal force exerted on the box by the floor? Solution System: Interactions: | Cloak |
|---|
| External influences from the earth (gravity), the floor (normal force) and the person (applied force). |
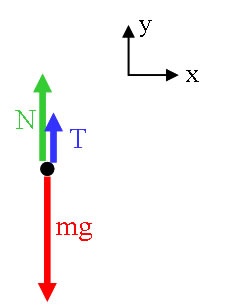
Model: Approach: Diagrammatic Representation We begin with a free body diagram for the box:  Image Added Image Added
Mathematical Representation From the free body diagram, we can write the equations of Newton's 2nd Law. | Latex |
|---|
\begin{large}\[\sum F_{x} = F_{A}\cos\theta = ma_{x}\]
\[ \sum F_{y} = N - mg - F_{A}\sin\theta = ma_{y}\]\end{large} |
Because the box is sliding over level ground, it is not moving at all in the y direction. Thus, it certainly has no y-acceleration. Setting ay = 0 in the y direction equation gives: | Latex |
|---|
\begin{large}\[ N - mg -F_{A}\sin\theta = 0 \]\end{large} |
Solving for the normal force gives: | Latex |
|---|
\begin{large}\[ N = mg + F_{A}\sin\theta = \mbox{ |
|