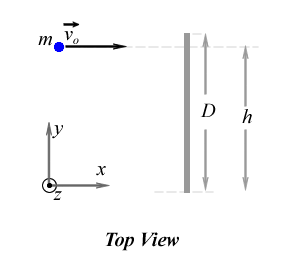
A uniform bar of mass M and length d is initially at rest on a horizontal and frictionless table. A ball of mass m and very small radius is moving towards the bar with speed vo, hits and sticks to the bar at a distance h measured from on end of the bar. The bar is not attached to the table and its moment of inertia with respect to its center of mass is known to be Icm. The goal of the problem is to
| Excerpt |
|---|
find the angular velocity and the velocity of the final object's (bar + ball) center of mass |
.
| Center |
|---|
 |
Solution
System: The ball is treated as a
point mass and the bar as a rigid body with its mass uniformly distributed.
Interactions: The system experiences
external interactions from the earth (
gravity) and the table's surface (only
normal force because the surface is frictionless). Since
gravity and the
normal force are both purely vertical forces in this problem, there are no
external horizontal
forces. For the same reason, there is no external
torque about
any vertical
axis of rotation.
Models: Angular Momentum and External Torque about a Single Axis and
Momentum and External Force.
Approach: Consider the MotionThe motion of the objects before and after the collision is on the table's surface, (x,y) plane. The coordinate system used in this problem is shown in the figure above. After the collision, the ball-bar system will translate to the right and rotate counter-clockwise about its center of mass which is not at the center of the bar but at some point between the ball and the center of the bar.
Because the rigid body translates and rotates we will apply linear momentum and impulse and angular momentum and angular impulse principles to the ball-bar system. For that purpose we need to calculate the sum of the external forces exerted on the system as well as the sum of the torques due to the external forces about a given point.
The Net External ForceThe external forces exerted on the system are the gravitational and the normal forces applied at the center of mass of the ball and the bar. Because there is no motion in the direction perpendicular to the table's surface (z-axis) the normal forces on both objects have the same magnitude but opposite direction than the respective gravitational forces. Therefore, the sum of the external forces on the system is zero and the linear momentum of the system is constant:
| Latex |
|---|
\begin{large}$\vec{P}^{before} = \vec{P}^{after}$ \end{large} |
The Net External TorqueThe net torque due to the external forces about a given point Q is given by:
| Latex |
|---|
\begin{large} $\sum \tau_{Q}^{ext} = \tau_{Q}^{mg} +\tau_{Q}^{N_{ball}} + \tau_{Q}^{Mg} +\tau_{Q}^{N_{bar}}$ \end{large} |
where the superscripts mg and Mg indicate the torques due to the gravitational force on the ball and the bar, respectively, and the superscripts Nball and Nbar the torques due to the normal force on the ball and bar, respectively.
We start by calculating the torques exerted on the ball. We choose an arbitratry point Q on the table and we measure the position of the ball's center of mass with the vector of magnitude r, the red arrow in the figure. The black arrows are the normal force and the gravitational force exerted on the ball of magnitudes Nball and FE on ball, respectively. Because these two forces are applied at the same point, the ball's center of mass, the corresponding moment arms are the same. In addition, these forces have the same magnitude but opposite direction, therefore the torques due to each of them also have the same magnitude and opposite direction and they add to zero. The torques are indicated with the purple vectors in the figure below.
| Center |
|---|
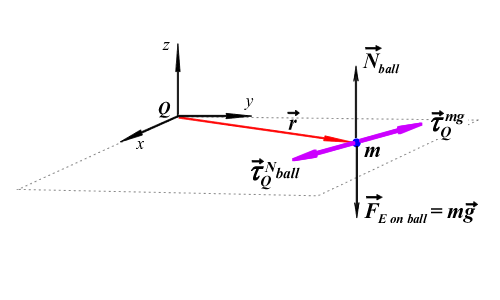 |
In the same way, we can calculate the torques due to the normal and the gravitational force exerted on the bar. These two forces are also applied at the same point, the centre of mass of the bar, therefore the moment arm about point Q is the same and because these two forces have the same magnitude but opposite direction the resulting torques about point Q will add to zero. We conclude that the sum of the torques due to the external forces on the system about point Q is zero, therefore that angular momentum of the ball-bar system about point Q is constant.
| Latex |
|---|
\begin{large} $ \vec {L}_{Q}^{before} =\vec L_{Q}$\end{large} |
| Note |
|---|
|
You can show that in this particular problem the net torque is zero about any point Q in space (not necessarily a point in the plane of the table). As a result, the angular momentum of the ball - bar system is constant about any point in space. |
Apply the Momentum and External Force ModelBefore the collision only the ball is moving then the linear momentum of the system is the linear momentum of a point particle of mass m moving with speed vo in the +x-direction:
| Latex |
|---|
\begin{large} $\vec P^{before} = m v\hat{x}$\end{large} |
After the collision the ball stays attached to the bar and they are both translating with the same velocity, the velocity of the center of mass of the system:
| Latex |
|---|
\begin{large} $\vec{P}^{after} = (m+M)\vec{v}_{cm}$\end{large} |
Because the sum of the external forces exerted on the system is zero the linear momentum is constant. Using the above expressions we obtain that the velocity of the center of mass is:
| Latex |
|---|
\begin{large}$\vec{v}_{cm} =\frac{mv_o}{m+M}\hat{x}$\end{large}(eq. 1) |
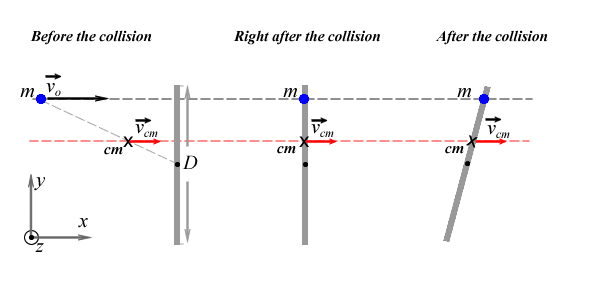
Also, because the sum of the external forces is zere the acceleration of the center of mass is zero, therefore the velocity of the center of mass is constant and the center of mass of the system moves along a stratight line (the x-component of the position of the center of mass increases linearly with time). In the figure below the motion of the the center of mass of the ball-bar system is hown. The center of mass is indicated with the black X and its path with a red dotted line. The centre of mass is a point somewhere between the ball and the center of mass of the bar. Note that only after the collision the center of mass is physically located inside the bar.
| Center |
|---|
 |
Apply the Angular Momentum and External Torque ModelBecause the net torque is zero about any point in space we have the freedom to choose it anywhere we want. Let's consider the point Q to be at some point below the lower end of the bar, at a perpendicular distance dQ from the bottom end as shown in red in the figure below.
| Center |
|---|
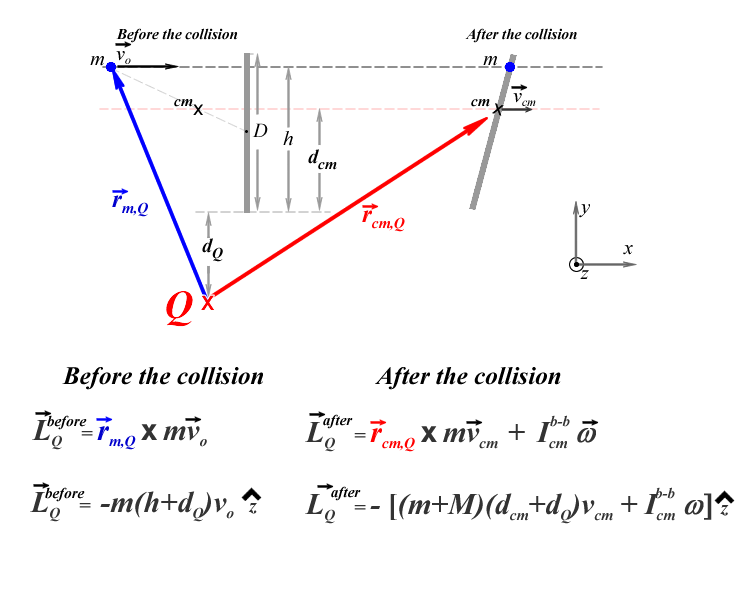 |
The distance between the bottom end of the bar and the straight dotted red line along which the center of mass of the system moves is defined as dcm and is given by:
| Latex |
|---|
\begin{large}$d_{cm}=\frac{mh+MD/2}{m+M}$\end{large} |
Before the collision only the ball is moving, therefore the angular momentum of the system is the angular momentum of a point particle moving along a straight line. The blue arrow in the figure of magnitude rm,Q is the position vector of the ball measured from point Q before the collision, so the angular momentum about point Q is given by:
| Latex |
|---|
\begin{large} $\vec L_{Q}^{before}=\vec{r}_{m,Q} $ x $m\vec{v}_{o} = -m (h+d_Q)v_o\hat{z}$\end{large} (eq. 2) |
where h+dQ is the distance between point Q and the straight line along which the ball moves.
After the collision both objects are rotating and translating as a rigid body (the ball is attached to the bar), therefore the angular momentum of the ball-bar system about point Q is the angular momentum of a rigid body rotating clockwise with angular speed ω and translating to the right with speed vcm. The position vector of the center of mass of the system measured from point Q after the collision has magnitude rcm,Q and is indicated in red in the figure, then the angular momentum of the system about point Q is given by:
| Latex |
|---|
\begin{large}$\vec L_{Q}^{after} = \vec{r}_{cm,Q} x (m+M)\vec{v}_{cm} + I_{cm}^{b-b}\vec \omega$\end{large} (eq. 3) |
where Icmb-b is the moment of inertia of the ball-bar system measured from the center of mass of the system and is given by:
| Latex |
|---|
\begin{large} $I_{cm}^{b-b} = I^{bar} + M(d_{cm}-D/2)^2 + m(h-d_{cm})^2$\end{large} (eq. 4) |
where Ibar = MD2/12 is the moment of inertia of the bar about its center of mass. To obtain (eq. 4) we used the parallel axis theorem. Both terms in (eq. 3) are vectors pointing in the -z-direction (into the paper) and can the translational part of the angular momentum can be expressed in terms of the distance between point Q and the straight line along which the center of mass is moving: :
| Latex |
|---|
\begin{large}$\vec L_{Q}^{after} = - ( (m+M)(d_{cm}+d_{Q})v_{cm} + I_{cm}^{b-b}\omega )\hat{z}$\end{large} (eq. 5) |
The angular momentum about point Q before and after the collision are equal, therefore setting (eq.3) and (eq.5) equal and with the help of (eq.1) we obtain that the angular velocity is given by:
| Latex |
|---|
\begin{large} $\omega = \frac{mv_{o}(h-d{cm})}{I_{cm}^{b-b}}$ \end{large}(eq. 6) |
Check your Answer| Tip |
|---|
|
Note that the answer does not depend on the choice of point Q. Check it! Choose the point Q at the center of mass of the ball-bar system or a point somewhere in the along which the ball is initially moving and you will obtain the same result as in (eq. 6) |
| Tip |
|---|
|
Note that the angular velocity is zero when h = dcm. Does it make sense? When does this happen? |
| Wiki Markup |
|---|
{html}
<MCE:SCRIPT type="mce-text/javascript"><#comment><#comment></#comment></MCE:SCRIPT>
<MCE:SCRIPT type="mce-text/javascript"><#comment><#comment></#comment></MCE:SCRIPT>
{html} |



