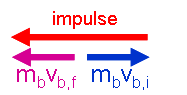Consider a ball of mass mb that is moving to the right at a constant speed vb when it suddenly impacts a wall and reverses direction (still moving at the same speed). What is the impulse delivered to the ball in the collision?
Solution
System: The ball as a
point particle.
Interactions: During the impact, we assume that the collision
force from the wall is vastly larger than any other
external forces on the ball, so that other forces are ignored.
Model: Momentum and External Force.
Approach:We will solve this problem using three different approaches to illustrate alternate ways to perform vector subtraction.
| Deck of Cards |
|---|
|
| Card |
|---|
| Using Algebra Diagrammatic Representation | Warning |
|---|
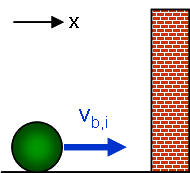
The magnitude of the momentum before and after the collsion is the same (mbvb), which can easily lead to the conclusion that there has been no change. Thinking about the situation, however, should quickly convince you that the ball has certainly been acted on by some force, which implies that a change did occur. Carefully drawing the initial-state final-state diagram below (taking special note of the coordinate system) shows the resolution to this difficulty. |
| 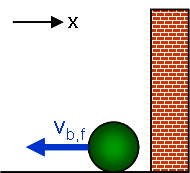
| Initial State | Final State |
|---|
The ball's initial x momentum is positive in our coordinates (+mbvb), while its final x momentum is negative (-- mbvb), giving a change of:
| Latex |
|---|
\begin{large}\[ J_{x} = -m_{b}v_{b} - m_{b}v_{b} = -2m_{b}v_{b}\]\end{large} |
where the negative sign indicates that the impulse is applied in the negative x direction, and so the impulse points leftward in this case.
| Card |
|---|
| Using Algebra |
|---|
| Using Algebra |
|---|
| |
| Card |
|---|
| label | Adding Vectors to get Final Momentum |
|---|
| |
Adding to get the Final MomentumWe have defined impulse as the final momentum minus the initial momentum, but subtracting vectors can be confusing. Therefore, we will first consider a rearrangement of the definition of impulse. We can write:
| Latex |
|---|
\begin{large}\[ \vec{p}_{f} = \vec{p}_{i} + \vec{J} \] \end{large} |
Thus, we can consider the impulse as the vector we must add to the initial momentum to yield the final momentum.
We can use this formulation to draw a vector diagram representing the ball-wall collision. Remembering the rules for adding vectors tail-to-tip, we can draw the following diagram which includes the impulse vector: 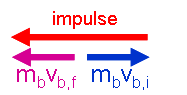
| Card |
|---|
| Adding Vectors to get Final Momentum |
|---|
| Adding Vectors to get Final Momentum |
|---|
| |
| Card |
|---|
| label | Subtracting Initial Momentum Vector from Final |
|---|
| |
Subtracting Initial Momentum from FinalIt is also possible to draw a vector representation of the regular definition of impulse
| Latex |
|---|
\begin{large}\[ \vec{J} = \vec{p}_{f} - \vec{p}_{i} \] \end{large} |
but drawing a vector equation that includes subtraction is tricky. We must think of this equation in the following way:
| Latex |
|---|
\begin{large}\[ \vec{J} = \vec{p}_{f} + (- \vec{p}_{i}) \] \end{large} |
In other words, we must think of the right hand side as the final momentum plus the negative of the initial momentum vector. Since the negative of a vector is just the reversed vector, this leads to the picture:

which gives the same impulse vector as the diagram above.
|
|