Shoemaker-Levy Comet Fragment 9 impacting Jupiter July 22 1994 |
Jupiter, showing the impact marks from fragments of Comet Shoemaker-Levy 9 in July 1994 |
Because gravity (interaction) will act to pull meteors, comets, and other space debris toward a planet, the effective cross-section for a planet to capture an object is larger than its geometrical cross-section. What is the size of this effective cross-section in terms of the physical qualities of the planet and the situation? What features of the impacting body is it independent of?
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representation
The initial situation with distances and velocities
The Force Diagram of the Meteor approaching the Planet
The torque (single-axis) about the center of the planet is zero, because the force of gravity (interaction) acts along the same direction as the radius r. About this point, therefore, angular momentum about a single axis is conserved.
Positions and velocity final:
Mathematical Representation
We can calculate the effective Capture Radius b by setting this as the distance the path of the mass is displaced from one running through the center of the planet for the situation where the mass just touches the surface of the planet at its closest approach. The offset between the path of the object and the center of the planet is usually called the impact parameter, and we are looking for its critical value. Once we have it, we can turn it into a cross-section for capture by squaring it and multiplying by π .
We begin by recognizing that both Energy and Angular Momentum (about the planet's center) are conserved. Some of the object's gravitational Potential Energy is transformed into Kinetic Energy, but none is lost. And since there is no torque when the Angular Momentum is calculated about the center of the planet, the angular momentum must be conserved as well. (Both of these statements would not be true if some nonconservative, dissipative Force was present, but we are assuming motion through empty space, and a fall onto a surface with no atmosphere.)We write the conditions for the initial state (when the mass is very far from the planet) with subscript i and for the final state (when the mass comes down and just grazes the planet tangentially) by the subscript f.
The mass of the meteor is m. That of the planet is M. The initial distance between the center of the planet and the meteor is ri. The final disttance is the radius of the planet, R.
The magnitude of the initial angular momentum is

The initial Energy is

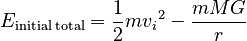
The final angular momentum is

And the final Energy is

Equating the two expressions for angular momentum gives


Inserting this into the expression for the final Energy, and equating the initial and final energies gives, after some algebra:
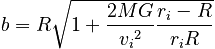
In the limit as ri goes to infinity, this becomes

The Capture cross-section is then
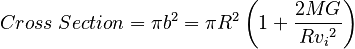
Looking either at the value of b or of the Capture Cross Section, we see that it goes toward radius R or area πR2 when the mass M goes to zero, or if G were to magically become zero, or if the initial velocity vi is much larger than MG .
On the other hand, the value of b (and of the Capture Cross Section) increases as the gravitational force of the planet increases (that is, as MG gets larger).
An unexpected result is that the value of b increases if MG remains the same but the value of vi decreases. When the initial velocity is zero, b becomes infinite, meaning that the meteor must invariably fall into the planet.
(Of course, this result assumes a universe consisting solely of a motionless meteor and a motionless planet, and nothing else. As soon as we add other masses, or any relative velocity, the result is different.)
Finally, note that the end result is completely independent of the mass of the meteor m . The Capture Cross-Section is the same for any mass falling into the planet at initial velocity vi .
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>

