Speed Trap

A common type of kinematics problem involves one person or object catching up to another person or object. Here we illustrate a few typical variations of this problem.

Part A

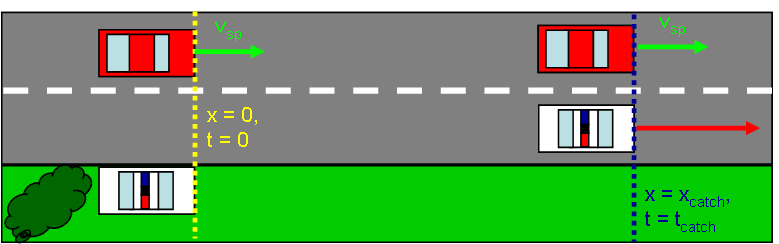
A speeder driving with a constant speed of 24.5 m/s approaches a (hidden) stationary police car on a long, straight road. The police officer detects the speeder using radar, and so the instant the speeder passes the police car, it begins accelerating after the speeder at a rate of 5.00 m/s². How long will it take for the police car to catch up to the speeder from the instant its acceleration begins?

Solution

Systems:

There are two separate systems here. Both the police car and the speeder's car will be treated as point particles.

Interactions:

Models:

Approach:

We will write an expression for the position of each vehicle as a function of time and then set the positions equal to each other. Since we have the freedom to pick our coordinate system, we can help ourselves in this problem by choosing the positive direction to be the direction of motion and setting x = 0 and t=0 at the point when the speeder passes the police car.

The key to any catch-up problem is that the catch-up occurs when the two systems have the same position.

The appropriate Law of Change for the speeder is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[x_

Unknown macro: {rm sp}

= x_

Unknown macro: {rm sp,i}

+ v_

t ] \end

where the subscript "sp" stands for "speeder".

The appropriate Law of Change for the police car is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ x_

Unknown macro: {rm pc}

= x_

Unknown macro: {rm pc,i}

+ v_

t + \frac

Unknown macro: {1}

Unknown macro: {2}

a_

t^

Unknown macro: {2}

]\end

where "pc" stands for "police car".

Before setting these equations equal to each other, it is a good idea to substitute the zeros so that we can cancel some of the many terms. In this problem, we have chosen our axis in such a way as to make x_sp,i = x_pc,i = 0. We also know that v_pc,i = 0 because the police car was at rest before the speeder passed it.

Although we suggest you solve problems symbolically before substituting numerical values, we make an exception for zeros. Using the zeros of the problem can result in dramatic simplification of the algebra.

Doing this and setting x_sp = x_pc gives:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {rm sp}

t = \frac

Unknown macro: {1}

Unknown macro: {2}

a_

Unknown macro: {rm pc}

t^

] \end

This is actually a quadratic equation in t, except that the constant term is absent. To be clear, we can rearrange:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \frac

Unknown macro: {1}

Unknown macro: {2}

a_

Unknown macro: {rm pc}

t^

- v_

Unknown macro: {rm sp}

t = 0 ] \end

This equation has two roots, which are easily obtained by factoring:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ t_1 = 0] [ t_

Unknown macro: {2}

= \frac{2 v_{\rm sp}}{a_{\rm pc}} ] \end

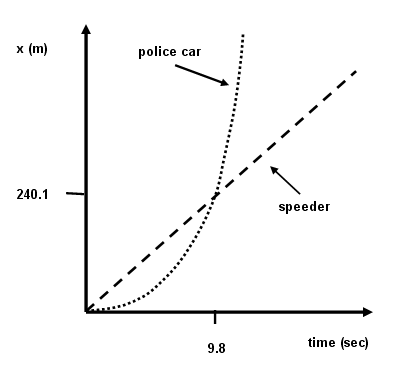
Recognizing that t = 0 is a root is actually a nice confirmation of our model. We have been trying to construct an equation that tells us when the police car and the speeder share the same position. Clearly, they do share the same position at t=0 since the speeder was passing the police car. If this root was absent, we should question the validity of our equation!

We select the second root, since we are interested in the time that the police car catches up to the speeder, not the time that the speeder passes the police car. Thus, we find:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ t = \frac{2 v_{\rm sp}}{a_{\rm pc}} = 9.8\;

Unknown macro: {rm s}

] \end

One way to help visualize the situation is the plot separately the position of the speeder and of the police car on the same graph of position vs. time

Unknown macro: {latex}

\begin

Unknown macro: {large}

[x_

Unknown macro: {rm sp}

= v_

t]\end

Unknown macro: {latex}

\begin

Unknown macro: {large}

[x_

Unknown macro: {rm pv}

=\frac

Unknown macro: {1}

Unknown macro: {2}

a_

Unknown macro: {rm pc}

t^2]\end

This model could be realistic for speed traps on roads with low speed limits, but it is unlikely to be a good description of a highway chase. Looking at our solution for the time of pursuit, consider how fast the police car will be going when it catches the speeder. Is this realistic for highway speeds?

Part B

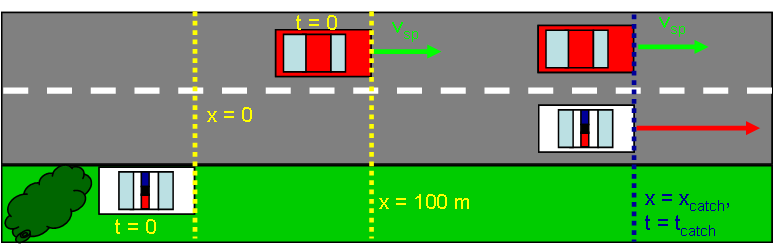
Again, a speeder driving with a constant speed of 24.5 m/s approaches a (hidden) stationary police car on a long, straight road. The police officer detects the speeder using radar, but this time the police officer begins accelerating at a rate of 5.00 m/s² only after the speeder has progressed 100 m down the road (the speeder has a 100 m head start). How long will it take for the police car to catch up to the speeder from the instant its acceleration begins?

Solution

Systems, Interactions and Models: The same as for Part A.

Approach:

The key difference from Part A is that we can no longer set up our position axis so that both cars are at position x = 0 if we want t=0 to denote the time that the police car begins the chase. Two choices for x=0 are the most common: place it at the speeder's position when the chase begins or place it at the police car's position when the chase begins. We will choose to place x=0 at the police car's position. Then, since the speeder is 100 m ahead, x_sp,i = +100 m.

We now follow the same procedure as in Part A, except retaining x_sp,i as a non-zero value. This gives:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ x_

Unknown macro: {rm sp,i}

+ v_

Unknown macro: {rm sp}

t = \frac

Unknown macro: {1}

Unknown macro: {2}

a_

Unknown macro: {rm pc}

t^

] \end

The net result is that we now have a quadratic equation that must be solved via the quadratic equation, rather than by simply factoring out a t. The answer is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[t = \frac{v_

Unknown macro: {rm sp}

\pm \sqrt{v_

^

Unknown macro: {2}

+2a_

Unknown macro: {rm pc}

\:x_

Unknown macro: {rm sp,i}

}}{a_{\rm pc}}]\end

The plus sign must be chosen to give a time greater than zero, so we find:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[t=\frac{v_

Unknown macro: {rm sp}

+\sqrt{v_

^

Unknown macro: {2}

+2a_

Unknown macro: {rm pc}

\:x_

Unknown macro: {rm sp,i}

}}{a_{\rm pc}} = 12.9\;

Unknown macro: {rm s}

]\end

You should check that the quadratic equation here matches the answer to Part A in the case that x_sp,i = 0.

In contrast to Part A, the second root in Part B is unphysical. The equation assumes that the police car is moving with constant acceleration. That assumption is only valid after t = 0, so the time given by the negative root will not represent the time that the speeder passed the police car. This is easily checked, since you know that the actual time the speeder passed the police car should be t = -100 m / (24.5 m/s) given what we are told in the problem. Does this match the negative root of the quadratic?

Unknown macro: {table}

Unknown macro: {tr}

Unknown macro: {td}

[Examples from Kinematics]

Unknown macro: {tr}

Unknown macro: {td}

The root page Examples from Kinematics could not be found in space Modeling Applied to Problem Solving.

Unknown macro: {search-box}

Child pages

Speed Trap

Part A

Solution

Part B

Solution