Part A
Suppose a 10 kg cubic box is at rest on a horizontal surface. There is friction between the box and the surface characterized by a coefficient of static friction equal to 0.50. If one person pushes on the box with a force F1 of 25 N directed due north and a second person pushes on the box with a force F2 = 25 N directed due south, what is the magnitude and direction of the force of static friction acting on the box?
Solution
System:
Box as point particle.
Interactions:
External influences from the earth (gravity) the surface (normal force and friction) and the two people (applied forces).
Model:
Approach:
Diagrammatic Representation
To determine the force of static friction, we first find the net force in the absence of friction. We first draw the situation. A top view (physical representation) and a side view (free body diagram) of the box ignoring any contribution from friction are shown here.
Mathematical Representation
The net force parallel to the surface in the absence of friction is then:
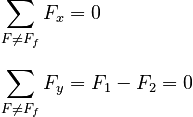
Thus, the net force along the surface is zero without the influence of static friction, and so the static friction force will also be 0.
Part B
Suppose a 10 kg cubic box is at rest on a horizontal surface. There is friction between the box and the surface characterized by a coefficient of static friction equal to 0.50. If one person pushes on the box with a force F1 of 25 N directed due north and a second person pushes on the box with a force F2 = 25 N directed due east, what is the magnitude and direction of the force of static friction acting on the box?
Solution
System:
Box as point particle.
Interactions:
External influences from the earth (gravity) the surface (normal force and friction) and the two people (applied forces).
Model:
Approach:
Diagrammatic Representation
To determine the force of static friction, we first find the net force in the absence of friction. We first draw the situation. A top view (physical representation) and a side view (partial free body diagram) of the box ignoring any contribution from friction are shown here.
Mathematical Representation
The net force parallel to the surface in the absence of friction is then:
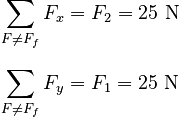
In order to prevent the box from moving, then, static friction would have to satisfy:
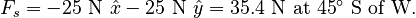
We're not finished yet!
We must now check that this needed friction force is compatible with the static friction limit. Newton's 2nd Law for the z direction tells us:
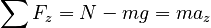
Note that friction from an xy surface cannot act in the z direction.
We know that the box will remain on the surface, so az = 0. Thus,
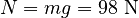
With this information, we can evaluate the limit:
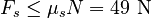
Since 35.4 N < 49 N, we conclude that the friction force is indeed 35.4 N at 45° S of W.
Part C
Suppose a 10 kg cubic box is at rest on a horizontal surface. There is friction between the box and the surface characterized by a coefficient of static friction equal to 0.50. If one person pushes on the box with a force F1 of 25 N directed due north and a second person pushes on the box with a force F2 = 25 N also directed due north, what is the magnitude and direction of the force of static friction acting on the box?
Solution
System:
Box as point particle.
Interactions:
External influences from the earth (gravity) the surface (normal force and friction) and the two people (applied forces).
Model:
Approach:
Diagrammatic Representation
To determine the force of static friction, we first find the net force in the absence of friction. We first draw the situation. A top view (physical representation) and a side view (free body diagram) of the box ignoring any contribution from friction are shown here.
Mathematical Represenatation
The net force parallel to the surface in the absence of friction is then:
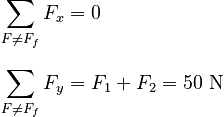
In order to prevent the box from moving, then, static friction would have to satisfy:
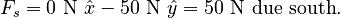
Again, we must check that this needed friction force is compatible with the static friction limit. Again, Newton's 2nd Law for the z direction tells us:
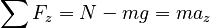
and know that the box will remain on the surface, so az = 0. Thus,
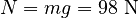
With this information, we can evaluate the limit:
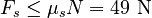
Since 50 N > 49 N, we conclude that the static friction limit is violated. The box will move and kinetic friction will apply instead!


