Down the Alley

Photo courtesy Wikimedia Commons, by user Fir0002

When a ball is started out with a purely sliding motion on a slick surface like a bowling alley, it will gradually begin to rotate until eventually (if the lane is long enough) it is rolling without slipping. Suppose a bowling ball which is effectively a solid sphere with a diameter of 22 cm and a mass of 6.0 kg is started down a perfectly level alley with a coefficient of kinetic friction equal to 0.10. The ball is initially sliding with no rotation and is moving at a rate of 2.8 m/s. How fast will the center of mass of the ball be moving along the alley when it is rolling without slipping?

Solution

We will solve the problem via three different methods.

Method 1

System: The ball as a rigid body.

Interactions:

Model: [1-D Angular Momentum and Torque].

Approach:

Diagrammatic Representation

We begin with a free body diagram. Since this problem will deal with rotation, we must also select an axis of rotation.

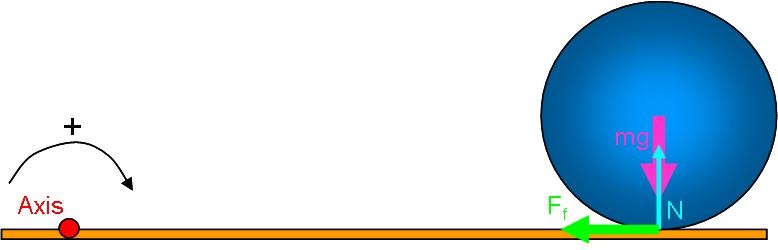
In this case, the most direct (but probably not the most obvious) method of solution is to consider the angular momentum about an axis fixed at some point on the alley surface. For simplicity, we select the point at which the ball is released. By taking a point on the alley surface, we have guaranteed that there is zero net torque acting on the system (the ball) about this axis. Gravity and the normal force each create a nonzero torque, but they balance each other perfectly because they share the same moment arm and they have the same magnitude. The friction force produces no torque because it has zero lever arm.

If it is not apparent to you that the force of gravity and the normal force acting on the ball have equal magnitudes, you should write Newton's 2nd Law for the y-direction.

Mathematical Representation

The [angular momentum (one-dimensional)] of the ball about the axis we have chosen can be broken into two parts by considering the contribution of the translation of the ball's center of mass and the rotation of the ball about its center of mass.

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ L = L_

Unknown macro: {rm trans}

+ L_

Unknown macro: {rm rot}

= mv + I\omega ] \end

Since there is zero net torque acting on the ball, the angular momentum is conserved and we can write:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ mv_

Unknown macro: {f}

+ I\omega_

= mv_

Unknown macro: {i}

+I\omega_

] \end

We know that ω_i = 0, and we also know that the ball ends up rolling without slipping. Thus, we know that:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \omega_

Unknown macro: {f}

R = v_

]\end

Thus, we have:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {f}

= \frac{v_{i}}{1+\frac

Unknown macro: {displaystyle I}

{\displaystyle mR^

Unknown macro: {2}

}} = \frac{v_{i}}{1+\frac

Unknown macro: {displaystyle 2}

{\displaystyle 5}} = \frac

Unknown macro: {5}

Unknown macro: {7}

v_

Unknown macro: {i}

= \mbox

Unknown macro: {2.0 m/s}

]\end

Method 2

System:

The ball as a rigid body.

Interactions:

External forces of gravity, normal force and kinetic friction.

Model:

Rotation and Translation of a Rigid Body and One-Dimensional Motion with Constant Acceleration.

Approach:

We can also approach this problem by the standard technique of treating the linear dynamics of the center of mass and the rotational dynamics of the ball about its center of mass separately. The free body diagram is the same as for method 1, but now we are calculating the torques about the center of mass of the ball. Gravity and the normal force will still produce no torque, but friction will have a non-zero lever arm, and hence produce a non-zero torque.

Thus, Newton's 2nd Law takes the form:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ - F_

Unknown macro: {f}

= ma_

Unknown macro: {x}

]\end

and its angular counterpart is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ F_

Unknown macro: {f}

R = I\alpha ] \end

The trouble is that these equations do not involve the speed of the ball. One way to bring the speed in is to use kinematics. We know that:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {x,f}

= v_

Unknown macro: {x,i}

+ a_

Unknown macro: {x}

t ][ \omega_

Unknown macro: {f}

= \omega_

Unknown macro: {i}

+ \alpha t]\end

Using the fact that ω_i = 0 and ω_f R = v_x,f and substituting for a_x and α using the equations we wrote above, it is possible to put these equations in the form:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {x,f}

= v_

Unknown macro: {x,i}

- \frac{F_{f}}

Unknown macro: {m}

t ] [ v_

= \frac{F_

Unknown macro: {f}

R^2}

Unknown macro: {I}

t ] \end

Eliminating t from the equations gives:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {x,f}

(1+\frac

Unknown macro: {I}

{mR^{2}}) = v_

Unknown macro: {x,i}

]\end

The same answer as was obtained using method 1.

Method 3

System:

The ball as a rigid body.

Interactions:

External forces of gravity, normal force and kinetic friction. Gravity is conservative while the normal force and friction are non-conservative.

Model:

Mechanical Energy and Non-Conservative Work, One-Dimensional Motion with Constant Acceleration and Point Particle Dynamics.

Approach:

Often when a speed is required, energy is an efficient way to obtain the answer. In this particular problem, angular momentum is a much faster route, but it is instructive to consider the form of the energy equations.

As the ball rolls along the alley, its height is not changing and so the gravitational potential energy is fixed (and so can be set to zero). The normal force is perpendicular to the ball's linear movement and also has no moment arm about the ball's center of mass, and so does no work that would affect the ball's linear velocity or its angular velocity. Friction, however, is anti-parallel to the ball's displacement and so it does negative work on the ball's rotational kinetic energy and it has a non-zero lever arm so it does work that acts to increase the ball's angular speed. The appropriate form of the mechanical energy equation is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ W_

Unknown macro: {nc}

+E_

Unknown macro: {i}

= -F_

Unknown macro: {f}

x+F_

R\theta + \frac

Unknown macro: {1}

Unknown macro: {2}

mv_

^

Unknown macro: {2}

+ \frac

Unknown macro: {1}

I\omega_

Unknown macro: {i}

^

Unknown macro: {2}

= E_

Unknown macro: {f}

=\frac

Unknown macro: {1}

mv_

Unknown macro: {f}

^

Unknown macro: {2}

+ \frac

Unknown macro: {1}

I\omega_

^

Unknown macro: {2}

]\end

Note that friction contributes two forms of non-conservative work, one from the linear motion and one from the rotational motion of the ball.

It is very important to recognize that mechanical energy is not conserved in this problem. The ball is not rolling without slipping, it is sliding and rotating. Thus, the friction is not static and so it does dissipate some mechanical energy into heat. For examples where pure rolling without slipping gives conservation of mechanical energy even in the presence of friction see, e.g.:

Error formatting macro: contentbylabel: com.atlassian.confluence.api.service.exceptions.BadRequestException: Could not parse cql : null

Once again, we know that ω_f R = v_f. We do not, however, know any relationship between x and θ at this time. The ball ends up rolling without slipping, giving the relationship between the final speeds, but it has certainly been slipping in the interim. Thus, the angular distance covered will not be directly related to the linear distance. To solve this problem, we must assume that the acceleration and angular acceleration are constant. In that case, we know from kinematics that:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ x = \frac{v_

Unknown macro: {f}

+ v_{i}}

Unknown macro: {2}

t ] [ \theta = \frac{\omega_

+ \omega_{i}}

Unknown macro: {2}

t]\end

We also know, as was used in Method 2, above, that:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[a_

Unknown macro: {x}

= - \frac{F_{f}}

Unknown macro: {m}

= \frac{(v_

Unknown macro: {f}

- v_

Unknown macro: {i}

)}

Unknown macro: {t}

]\end

Substituting appropriately into the energy equation and using the rolling without slipping condition then gives the same answer as was obtained via methods 1 and 2.

It is instructive to note that the (negative) work done by friction on the linear kinetic energy is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ -F_

Unknown macro: {f}

x = -F_

\frac{v_

Unknown macro: {f}

+v_{i}}

Unknown macro: {2}

t ]\end

while the positive work done in increasing the angular kinetic energy is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ F_

Unknown macro: {f}

R\theta = F_

\frac{v_{f}}

Unknown macro: {2}

t ] \end

Clearly, the negative work is larger in magnitude, and we can see that the net energy dissipated to heat will be:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ |W_

Unknown macro: {rm dissipated}

| = F_

Unknown macro: {f}

\frac{v_{i}}

Unknown macro: {2}

t ] \end

where t is the amount of time elapsed from the instant the ball is released until the instant it begins to roll without slipping.

Child pages

Down the Alley

Solution

Method 1

Method 2

Method 3