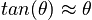A very useful approximation for many physical applications, especially for simple harmonic motion and pendulums in particular. It states that when the angle is small, and expressed in radians, then we may approximate sin(θ) by θ. At the same time, we may approximate cos(θ) by 1 and tan(θ) by θ.
This follows because the sine function may be expressed as the infinite Taylor series:
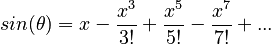
If the angle is small enough, then we can ignore all but the first term, giving
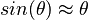
This gives us our criterion for "small enough", because it is clear that this will be the case when x is much greater than x3/3!, or in other words 6 >> x2.
Similarly, the Taylor series for cos(θ) is
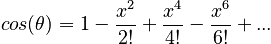
so that in the small angle approximation we have
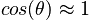
Finally, the expansion for the tangent is
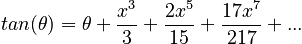
So that for small angles