Some modern roller coasters are "launched" rather than slowly pulled to the top of a hill. One recent design is a coaster on a U-shaped track like that shown above. Each time the coaster passes through the acceleration zone, it receives a kick from an electric motor. Suppose that for the track shown above, the height H is 75 m. The acceleration zone has a width d = 25 m. If a coaster of mass m = 11,000 kg experiences an accelerating horizontal force of magnitude 0.5mg while it is in the acceleration zone, how many passes through the zone must the coaster make before it will reach the top of the track? (After this, the function of the motor will be reversed to decelerate the coaster.)

Solution

System:

Coaster as point particle, plus the earth as a rigid body of infinite mass.

Interactions:

The coaster and earth create a conservative interaction of gravity, which will be treated as a potential energy in the system. The system is also subject to a non-conservative interaction from the the electric motor.

Model:

Mechanical Energy, External Work, and Internal Non-Conservative Work.

Approach:

Diagrammatic Representation

We begin with an initial-state final-state diagram and energy bar graphs.

Initial

Final

Mathematical Representation

It is clear from the diagrammatical representations that the system has gained mechanical energy. The source of the energy is the electric motor. In equation form, we have:

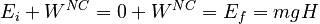
where the non-conservative work is due to the motor.

From the definition of work, the work done by the motor can be related to the force provided by the motor:

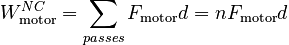
where n is the number of passes the train makes through the acceleration zone. Since the force provided by the motor is 0.5mg, we can write:

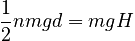
which is solved to obtain:

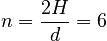
which implies the coaster must make 6 complete passes through the acceleraation zone to reach the top of the track.

Technically this implies our initial-state final-state diagram was wrong, since we drew the coaster on the wrong side of the track. Remember that diagrams in physics problems are often useful, even if some details of the problem are not completely understood. They are meant to provide a summary of the physics concepts involved, not necessarily a mathematically precise statement of the problem.