An Exercise in Continuity

Suppose an object is moving along a one-dimensional position axis. The object starts its motion at t = 0 at the position x = 0 and with velocity v = 0. It has an acceleration of +2.0 m/s². After 4.0 seconds, the object's acceleration instantaneously changes to - 2.0 m/s². Plot velocity and position versus time graphs for the first 8.0 seconds of the object's motion.

Solution

System:

The object will be treated as a point particle.

Interactions:

The accelerations as described in the problem.

Model:

One-Dimensional Motion with Constant Acceleration, applied twice to cope with the change in acceleration.

Approach:

Understand the Limitations of the Model

We will have to use the model twice. Even though the acceleration has a size of 2.0 m/s² throughout the motion, the direction of the acceleration changes at t = 4.0 s. Therefore, the acceleration is not constant over the first 8 seconds of the motion. The acceleration is, however, separately constant in the time intervals from 0 to 4 seconds and from 4 to 8 seconds. We will therefore have to use the model twice: once to describe the motion from t = 0 seconds to t = 4.0 seconds, and once more to describe the motion from t = 4.0 seconds to t = 8.0 seconds.

The First Interval

For the first part of the motion, our givens are:

givens

We begin by finding the velocity. The simplest Law of Change appropriate to our givens is:

which, after substituting the givens, tells us:

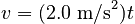
This is the equation for a line with slope 2 and intercept 0, giving the graph:

We then find the position. The most direct Law of Change is:

which yields the parabolic graph:

The Second Interval

We now wish to analyze the second part of the motion. In this part of the motion, we must change our givens. We now have t_i = 4.0 s, t = 8.0 s, and a = – 2.0 m/s². Unfortunately, this is not enough. We do not know x_i, x, v_i or v. We have too few givens to proceed.

The answer to this dilemma is simple. We have just derived expressions that give x and v for any time between 0 s and 4.0 s. We would like to know x and v at 4.0 s. Thus, we can use the final time of the first part of the problem to obtain the initial conditions for the second part. From our graphs or from the equations, we can complete our list of givens for the second part:

givens (second part)

This allows us to write an equation for the velocity:

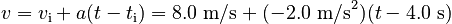
and the position:

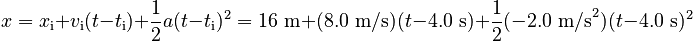
Putting them Together

These new expressions can be used to finish the plots we started in the first part. Plotting the functions from the first part in the interval t = 0 s to t = 4.0 s and the functions from the second part in the interval t = 4.0 s to t = 8.0 s gives the complete graphs shown below. For completeness, we also show the acceleration graph.

Here we can see that although the acceleration is discontinuous (has a break in the graph at t = 4.0 s) the velocity is not discontinuous. The velocity is a connected graph, though it does display a kink at 4.0 s, when the graph suddenly takes a sharp bend. This kink is a sign of a discontinuous 1st derivative (the 1st derivative of velocity with respect to time is acceleration, which is discontinuous). The position, however, is completely smooth. It is connected and displays no kinks. (The first derivative of position is velocity, which is continuous.)