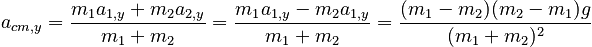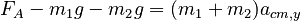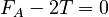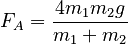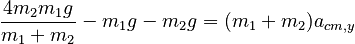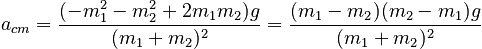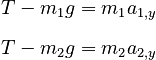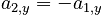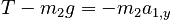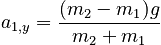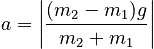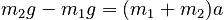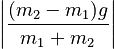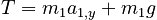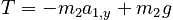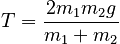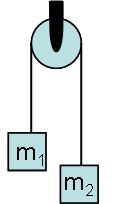
Atwood's Machine consists of two objects (of mass m1 and m2) hung over a pulley.
Part A
Treating the pulley as massless and frictionless and treating the rope as massless and of fixed length, find an expression for the accelerations of the two masses.
Solution
Atwood's Machine is an excellent example of a problem that can be dealt with using many different definitions of the system. We will solve it using two methods to showcase some of the pitfalls of constructing a system when a pulley is involved.
Method 1
Systems:
Object 1 as a point particle and object 2 as a separate point particle system.
Interactions:
Each system is subject to external influences from the earth (gravity) and the rope (tension).
Model:
Point Particle Dynamics.
Approach:
Diagrammatic Representation
We begin by treating each object separately. We construct free body diagrams:
where the force of tension on each of the objects is exactly the same magnitude. The direction of the force is upwards for both masses because the rope is wrapped around the pulley, and thus hangs downwards at each end (and pulls upward at each end).
Mathematical Representation
Using the free body diagrams as a guide, we write Newton's 2nd Law for each object. We consider only the y direction, since the x direction simply yields the equation 0 = 0. Because everything is in the y direction, we work with the magnitudes of the forces and explicitly include signs (rather than including lots of tedious "y" subscripts).
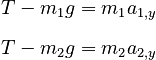
To finish this problem, we must use the constraint on the acceleration. The accelerations of objects 1 and 2 are constrained by the fixed length of the rope to be equal in size and opposite in direction. It makes sense to use this fact to eliminate one of the accelerations in the above equations and thus obtain a single expression for the other in terms of the gravitational constant g and the two masses. In our case, we arbitrarily substitute for a2 using:
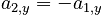
giving:
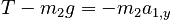
Eliminating the tension from the system of equations then gives:
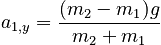
Since the accelerations are the same size, we can characterize the acceleration of the system as:
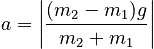
Method 2
A second method is to use a "math shortcut" by defining an unphysical system that replicates the mathematical features of the problem.
System:
Mathematical construction including the two objects and the rope connecting them.
Interactions:
External forces from gravity on each block.
Model:
Point Particle Dynamics.
Approach:
This method uses the fact that when a massless, frictionless pulley is involved, the pulley has essentially no role in the system except to change the direction of forces. Thus, the dynamics of Atwood's Machine are completely equivalent to the dynamics of the system sketched here:

Of course, this system is anything but physical. The important point is that the mathematics are identical. This trick of "straightening" the system is often useful when a massless, frictionless pulley is involved. Note that we have chosen to draw the system in the x direction instead of the y direction to remind us that gravity will not pull in the same direction on each mass! Thus, the free body diagram for the system looks like:
and the resulting form of Newton's 2nd Law is:
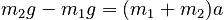
so that again, the magnitude of the acceleration is:
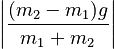
Error rendering macro 'deck'
java.lang.NullPointerException
Part B
Find the tension in the rope in terms of the object masses and the acceleration of gravity.
Solution
Systems:
As in Part A, Method 1.
Interactions:
As in Part A, Method 1.
Model:
As in Part A, Method 1.
Approach:
To find the tension, which is an internal force if we combine the two masses and rope into one system, we must return to the approach of Method 1, treating each object separately. From our work in Part A, we actually have two expressions for the tension:
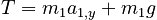
or
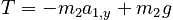
In either case, inputting our answer for a1,y yields:
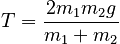
Part C
Part A makes it clear that the system of the two objects has an accelerating center of mass (provided the masses are not exactly equal). Using the results of Method 1, we can find the acceleration to be:
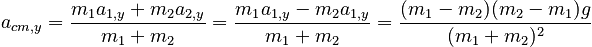
Show that this center of mass acceleration is consistent with the sum of the external forces on the system.
Solution
Systems:
The two objects, the pulley and the rope.
Interactions:
The system is subject to external forces from gravity and from the axle of the pulley. We will also have to consider the pulley as an independent point particle system acted upon by the rope (tension) and by the axle.
Method:
Point Particle Dynamics.
Approach:
Diagrammatic Representation
A truly physical approach that incorporates both objects into one system must also include the pulley. We begin with a picture and free body diagram for that system:
Mathematical Representation
We can now write Newton's 2nd Law for the system:
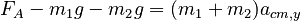
where acm is the acceleration of the system's center of mass.
To find FA, we must use the free body diagram for the pulley:
The pulley is not accelerating, so we have:
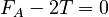
Thus, using the results of Part B, we have:
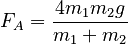
We can then substitute to find:
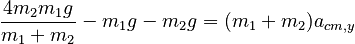
Which gives:
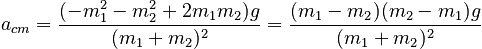
which agrees with the problem statement.
Note that it is impossible to understand the center of mass acceleration using our "mathematically equivalent" system of Part A Method 2.
Error rendering macro 'deck'
java.lang.NullPointerException