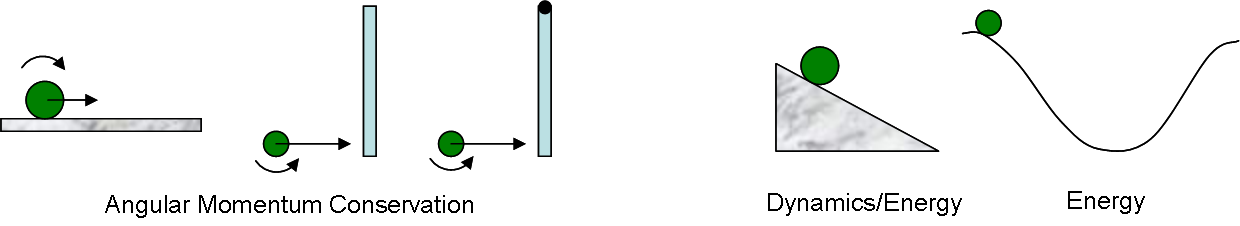Many students have asked about when to include center of mass motion when calculating angular momentum and energy. In this page, we give a discussion of some of the main issues.
Issue 1: Pure Rotation and the Parallel Axis Theorem
Recognizing Pure Rotation
One key idea in determining how to describe rotational problems is recognizing whether the problem can be treated as pure rotation. Whenever an object is spinning around a fixed axle, we can choose to describe that motion as pure rotation about the axle, even if the center of mass is not located at the axle.
Two Descriptions of Pure Rotation: The Parallel Axis Theorem vs. Rotation and Translation
An object moving in pure rotation about an axle can be described in two different but equivalent ways.
- The object is only rotating, but the moment of inertia about the fixed axle must be found using the parallel axis theorem.
- The object is rotating about the center of mass and its center of mass is translating.
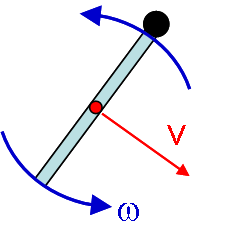
To see why these descriptions are equivalent, consider how we would find the angular momentum and kinetic energy of a bar pivoted at one end.
Method 1: The bar is purely rotating. We do not include any contribution from the CM motion.

Method 2: The bar is rotating about its CM and the CM is translating.

To see that Method 2 is equivalent to Method 1, we must realize that the center of mass speed is related to the rotational velocity of the bar by the distance of the CM from the axis of rotation:

You can now substitute this into the expressions for L and K:

which are equivalent to the expressions found in Method 1.
Parallel Axis Theorem and Dynamics
Generally it is advantageous use the parallel axis theorem and consider the motion to be pure rotation. The problem of the rod pivoted about one end is a good example of why. If you are asked to find the angular acceleration of the rod or to find the frequency of small oscillations, you will need to compute the torque around the pivot and set that torque equal to I times alpha. The appropriate moment of inertia to use is the moment of inertia about the end of the rod.
Issue 2: Rotation plus Translation and External or CM Axis
Dynamics, Energy Conservation, or Angular Momentum Conservation?
When deciding how to deal with an object that cannot be considered to be purely rotating, you must first decide whether you will be using angular momentum conservation. We know two basic situations that are often treated with angular momentum conservation and can involve a rotating and translating object:
- Collisions that result in rotation.
- Bowling balls or other objects rolling and slipping on a level surface.
Other situations must generally be dealt with using dynamics or energy conservation. The most common example is an object rolling on a ramp or track.
Angular Momentum Conservation requires Stationary Axis
Problems involving conservation of angular momentum essentially require that you choose a stationary axis that lies outside the objects involved. For the bowling ball, the axis must lie on the ground (see Down the Alley). For a collision, the axis is generally placed either at the fixed axis of the collision target (if it is attached to a pivot), at the level of the system CM for a free target that sticks to the incoming object, and at the level of the target CM for a free target that does not stick to the incoming object.
The angular momentum of a rotating and translating object about a stationary external axis is given by:

Dynamics or Conservation of Energy requires CM Axis
Problems involving dynamics or conservation of energy of an object rolling along a ramp or track are most easily solved by placing the axis of rotation at the object's center of mass. The translation of the center of mass and the rotation about the center of mass must then be considered separately. For dynamics, the translation will be governed by F = ma and the rotation will be governed by torque equals ICM times alpha. For energy, the kinetic energy of the object will be:

Note that if the object is rolling without slipping, the speed of the CM and the angular velocity of the rotation about the CM can be related by using the radius of the object.
Issue 3: Orbits
Background: Point Masses
Satellites in orbit are an excellent example of the point mass approximation. Their size and rotation are completely negligible when compared to the radius of the orbit and their orbital speed. Point masses have zero ICM. Thus, they never have two parts to their angular momentum or kinetic energy.
You can choose to write their angular momentum as:

or

where the last expression contains the part of v that is perpendicular to the radial line from the axis of rotation (the center of the planet for orbits).
These two expressions for the angular momentum are totally equivalent, because for a point mass

and

. Substituting these into the first equation for L will give the second equation.
The kinetic energy should simply be written as:

because the entire velocity contributes to the kinetic energy, not just the part perpendicular to the radial line. In a perfectly circular orbit (where the whole velocity is perpendicular to the radius), one-half m v squared is equivalent to one-half I omega squared, but in an elliptical orbit it is not.
Special Points: Extrema
The min and max distance from the planet in an elliptical orbit are special, because they are the only places that the velocity is exactly perpendicular to the radial line. Thus, the angular momentum at these extrema is easy:

<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>