You are viewing an old version of this page. View the current version.
Compare with Current
View Page History
« Previous
Version 28
Next »
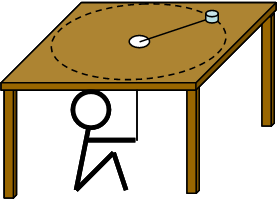
A small object with a mass of 0.250 kg has been attached to a massless string, and is moving in a circle on a perfectly level frictionless tabletop. The string passes through a hole in the center of the table, and is held by a person. Suppose that initially the mass is rotating with an angular speed of 15.0 rad/s around a circle of radius 0.400 m. The person then pulls the string in such a way as to reduce the radius of the circle at a constant rate. The person stops reducing the radius when the object is making a circle of radius 0.200 m. How much work did the person do in the course of reducing the radius of the circle?
Solution
We will approach the problem in two ways. First, we will use the change in mechanical energy to obtain the answer in a straightforward manner. We will then compare our answer to that obtained using the (considerably more complicated) method of computing the integral of the force times displacement along the path.
Method 1: Energy
System: The object as a point particle undergoing pure rotation.
Interaction: External forces from the string (tension, non-conservative), the earth (gravity, conservative) and the table (normal force, non-conservative).
Model: Angular Momentum and External Torque about a Single Axis plus Mechanical Energy, External Work, and Internal Non-Conservative Work.
Approach:
Consider the Energy
The table is level, so the gravitational potential energy will be constant. We can set it to zero by taking the height of the tabletop to be zero. The normal force is perpendicular to the motion of the object and so does no work. The only force capable of performing work on the object is the tension, which is equal to the force from the person pulling on the string. Thus, the work done by tension will equal the work done by the person. This work can be computed by finding the change in mechanical energy of the object:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ W^
Unknown macro: {NC}
+ E_
Unknown macro: {i}
= E_
Unknown macro: {f}
]\end
or, since the height of the object is constant throughout the motion and no spring is present:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ W^
Unknown macro: {NC}
= E_
Unknown macro: {f}
- E_
Unknown macro: {i}
= K_
- K_
Unknown macro: {i}
]\end
Because the object can be considered to be moving in pure rotation about the center of the circle, we can compute its kinetic energy using the rotational formula:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ K = K_
Unknown macro: {rm rot}
= \frac
Unknown macro: {1}
Unknown macro: {2} I\omega^
]\end
For a point particle,
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ I = mr^
Unknown macro: {2}
]\end
and so:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ W = \frac
Unknown macro: {1}
Unknown macro: {2}
m\left(r_
Unknown macro: {f}
^
\omega_
Unknown macro: {f}
^
\omega_
Unknown macro: {i}
^
Unknown macro: {2}
\right)]\end
Consider the Angular Momentum
We cannot yet substitute into the equation obtained by considering the object's energy. We do already have the initial and final radius of the motion, but we do not yet have the angular speed. To find it, we consider the torque on the system. We choose the natural location for the axis by locating it at the center of the circle.
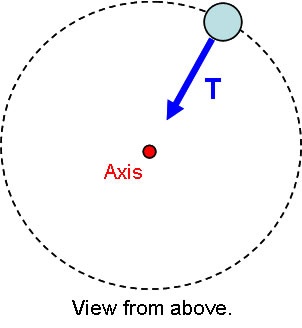
With this choice, we can see that there is zero net torque on the system, since the moment arm for the tension is zero. With the net torque equal to zero, we are in the special case of constant angular momentum, so:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ I_
Unknown macro: {f} \omega_
= I_
Unknown macro: {i} \omega_
]\end
By using the formula for the moment of inertia of a point particle, we can show:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ \omega_
Unknown macro: {f}
= \omega_
Unknown macro: {i}
\left(\frac{r_{i}}{r_{f}}\right)^
Unknown macro: {2}
]\end
Substituting into the work-energy theorem then gives:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ W = \frac
Unknown macro: {1}
Unknown macro: {2}
mr_
Unknown macro: {i}
^
\omega_
Unknown macro: {i}
^
Unknown macro: {2}
\left(\frac{r_
^{2}}{r_
Unknown macro: {f}
^{2}} - 1\right) =\mbox
Unknown macro: {13.5 J}
]\end
Method 2: Dynamics
System: The object as a point particle undergoing pure rotation.
Interactions: External forces from the string (tension), the earth (gravity) and the table (normal force).
Model: Point Particle Dynamics, Angular Momentum and External Torque about a Single Axis plus the definition of work.
Approach:
To move the object radially inward at constant speed, the tension force must simply provide the centripetal force.
We therefore have:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ T = m\omega^
Unknown macro: {2}
r ] \end
Since, as discussed in Method 1 above, the only force that does work is the tension, we can now use the definition of work:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ W = \int_{r_{i}}^{r_{f}} \vec
Unknown macro: {T}
\cdot d\vec
Unknown macro: {r}
= - \int_{r_{i}}{r_{f}} m\omega
Unknown macro: {2}
r\:dr]\end
Before we can evaluate this integral, we must determine the dependence of ω on r. As in Method 1, we make use of the fact that (if we choose the center of the circle for the axis of rotation) the angular momentum of the object is constant. Thus:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ I(r)\omega(r) = I_
Unknown macro: {i} \omega_
]\end
Or, by using the formula for the moment of inertia of a point particle:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ \omega(r) = \omega_
Unknown macro: {i}
\left(\frac{r_{i}}
Unknown macro: {r}
\right)^
Unknown macro: {2}
]\end
Inserting this formula into our expression for work gives:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ W = -\int_{r_{i}}^{r_{f}} m\omega_
Unknown macro: {i}
^
Unknown macro: {2}
r_
^
Unknown macro: {4}
r^{-3} \:dr = \frac
Unknown macro: {1}
Unknown macro: {2}
mr_
Unknown macro: {i}
^
\omega_
Unknown macro: {i}
^
Unknown macro: {2}
\left(\frac{r_
^{2}}{r_
Unknown macro: {f}
^{2}} - 1\right) ]\end


