Valid inequalities

Valid inequalities are additional constraints that can be added to a correct integer program that potentially strengthen the formulation, i.e. reduce the size of the feasible region for the linear programming relaxation.
For example, in the 0-1 knapsack problem,

for any set $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ such that

we can add the cover inequalities

To be completely concrete, suppose that $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, and our instance was

The feasible region of this LP and the feasible region of the integer hull are shown below.

Observing that $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, we can apply a cover inequality with the set $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ to obtain the inequality

Observe that adding this inequality to the knapsack formulation makes the LP relaxation integral, thus it is a stronger formulation.

User Cuts in CPLEX

User cuts are, at a high level, valid inequalities for an integer program CPLEX will optionally add while searching for an integer solution. Like lazy cuts, user cuts can be added either before the optimization begins (with addUserCut() from IloCplex) or by using a UserCutCallback (documentation here) to detect violated constraints on the fly and add them to the formulation. CPLEX checks for violated user cuts at the highlighted stage in the diagram below.

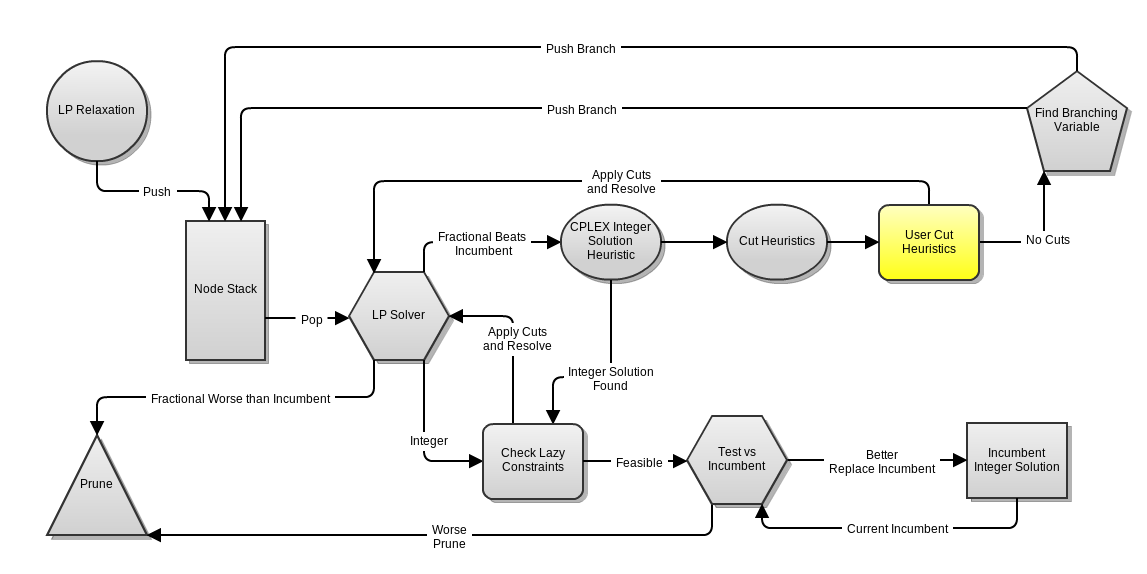
As you can see, there is no guarantee that a feasible solution will satisfy all of the user cuts, as LP solutions which are integral are sent through the lazy constraints to the incumbent. Thus if a constraint is necessary for the formulation to be correct, but you want to check for it as a user cut, you must also check for it as a lazy cut. Additionally, we have the benefit that our method for identifying user cuts doesn't need to work 100% of the time, as if it fails we always have the lazy cuts for insurance. This is how we will be using user cuts for our TSP solver.

Using UserCutCallback

UserCutCallback works very similarly to LazyConstraintCallback. Mathematically, you are passing CPLEX the following function:

• Input: A fractional solution to the LP relaxation of your problem, potentially after some lazy constraints, CPLEX generated cuts, or user cuts have been added
• Output: A list (potentially empty) of violated valid inequalities.

Note that there is no assumption that the list is is nonempty, and that there is no guarantee that the UserCutCallback will ever be checked. The Javadoc for UserCutCallback can be found here, but we summarize the important methods in the table below (the interface is very similar to that of LazyConstraintCallback):

The final method requires some explanation. The "cut loop" refers to the loop in the above diagram where CPLEX looks for cuts, adds cuts, and resolves the LP relaxation. While CPLEX could do this indefinitely until an optimal integer solution was found (which would solve the whole IP, see cutting plane method and chapter 9 of Optimization over the Integers), this would generally take a long time. Instead, CPLEX uses some internal Heuristics (which you can toggle, although I don't recommend it) to control how many cuts to add, then it "exits the cut loop" and will not generate more cuts. By calling isAfterCutLoop, you can tell if CPLEX is done adding cuts before you start adding your own. It might be a good idea to wait until CPLEX is done, as the cuts it adds may change the LP so much that the cut you were about to add becomes irrelevant. Alternatively, the cut you add may cause CPLEX to add smarter cuts. Whether or not waiting until the cut loop is over to add cuts is something that you will need to determine for your own problem.

Otherwise, the same warnings as before about using cplex.ge() instead of cplex.addGe() and using getValues() instead of getValue() are still relevant. In fact, the performance hit on using getValue() is much more severe here than for LazyConstraintCallback, as we will pay the price at every node, not just at every integer solution.

Polynomial Time Separation for TSP over Cutset Constraints

Given a fraction solution $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, we need a polynomial time algorithm that will find the most violated cutset constraint (as previously defined here),

This is known as the separation problem. If we take each $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ to be the weight of edge $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ and form a weighted subgraph of the original graph where every node is present, every edge $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ with $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ is present, and the weights are given by the $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, then we can solve this problem by finding the global minimum cut in the graph. A wide range of algorithms have been devised to solve this problem, e.g.

• A single larger max flow min cut computation by Hao and Orlin,
• A randomized contraction algorithm by Karger and Stein
• A simple deterministic algorithm by Stoer and Wagner that has been implemented (although not optimally) in JGraphT
• A variety of more modern improvements by Karger (2000, 2009) and other authors.
• See also here for implementation details of some of these algorithms

Instead we will take a much simpler approach. Fix some node $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, and observe that in every cut $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ must be on one side of the cut or the other. Thus it suffices to solve $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ minimum $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ cut problems, for each $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, $//<![CDATA[ \begin{array}{l}\end{array} //]]>$. Then if $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ is the minimum global cut, WLOG $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, then as $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, for some $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, when we compute the minimum $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ cut, we will have $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, so the result will be the global minimum cut.

TODO add a graphic.

Implementing UserCutCallback for the Cutset Constraints

Much like with LazyConstraintCallback, we will extend UserCutCallback with an innner class inside TspIpSolver. At the bottom of TspIpSolver.java (but before the final '}' ending the class), add the following code to extend UserCutCallback:

	private class MinCutCallback extends UserCutCallback{

		private double minCutVal;
		
		public MinCutCallback(){
			minCutVal = 1.99;
		}

		@Override
		protected void main() throws IloException {
			//fill this in
		}
	}

The value minCutVal is a numerical tolerance, we will only consider a constraint violated if the edges sum to less than 1.99 (the constraint says they should sum to at least 2.0). Next, we need to tell our solver to use the MinCutCallback, but only the option Option.userCut is selected. At the end of the constructor for TspIpSolver, add

		if(options.contains(Option.userCut)){
			cplex.use(new MinCutCallback());
		}

Recall previously that we defined a method getEdgesUsed() that takes an array of doubles, one for each edge, where it is assumed that each edge value is either zero or one, and returns the subset of the edges taking the value one. We need an analagous method for one the edge weights are fractional. Add the following method to TspIpSolver after getEdgesUsed()

	private Map<E,Double> getNonZeroEdgeWeights(double[] edgeValues){
		Map<E,Double> edgeWeights = new HashMap<E,Double>();		
		for(int i = 0; i < edgeValues.length; i++){
			if(edgeValues[i] > Util.epsilon){
				edgeWeights.put(edgeVariables.inverse().get(edgeVariablesAsArray[i]), edgeValues[i]);
			}
		}
		return edgeWeights;
	}

Given the edge weights, assumed to be in the order of the edge array edgeVariablesAsArray, this method returns a Map taking edges to their weight, but edges with weight zero are excluded.

Now you need to fill in the method main() from the callback, which should check to see if the current fractional solution violates any cutset constraints, and if so, add those constraints. Here is an outline of one possible solution:

1. Exit (by returning) if we are not yet out of the "cut loop."
2. Get a double[] of all the edge variable values
3. Convert this into a Map<E,Double> containing only those edges taking the value greater than zero.
4. Form a subgraph of these edges.
5. Fix a node $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, then for every other $//<![CDATA[ \begin{array}{l}\end{array} //]]>$, compute the minimum $//<![CDATA[ \begin{array}{l}\end{array} //]]>$ cut.
6. For every cut with weight less than minCutVal (1.99), find all edges across the cut (including edges with weight zero that were not in the subgraph)
7. For each of these edge sets, add a new cutset constraint to the model.

Code has been provided to perform step 3 with getNonZeroEdgeWeights() and to aid in steps 4-6. In particular, we provide the class MinCutSolver which has the constructor

and the method

The following methods and fields should all be useful

• edgeVariablesAsArray, from TspIpSolver which you can apply getValues() directly to.
• cutEdges() from TspInstance
• integerSum() from Util
• calcSum() from Util

Solution

	private class MinCutCallback extends UserCutCallback{
		
		private double minCutVal;
		
		public MinCutCallback(){
			minCutVal = 1.99;
		}

		@Override
		protected void main() throws IloException {
			//do not attempt to add any cutset constraints until CPLEX is done adding constraints
			if(!this.isAfterCutLoop()){
				return;
			}
			double[] edgeVals = this.getValues(edgeVariablesAsArray);
			Map<E,Double> edgeWeights = getNonZeroEdgeWeights(edgeVals);
			UndirectedGraph<V,E> graph = tspInstance.getGraph();
			MinCutSolver<V,E> minCutSolver = new MinCutSolver<V,E>(graph,edgeWeights);
			Set<Set<E>> cutSets = new HashSet<Set<E>>();
			V source = graph.getVertices().iterator().next();
			for(V sink : graph.getVertices()){
				if(sink != source){
					Set<V> cutNodes = minCutSolver.computeMinCut(source, sink);
					Set<E> cutEdges = tspInstance.cutEdges(cutNodes);
					double cutVal = Util.calcSum(cutEdges,edgeWeights);
					if(cutVal < minCutVal){
						cutSets.add(cutEdges);
					}
				}
			}
			for(Set<E> cutEdges: cutSets){
				this.add(cplex.ge(Util.integerSum(cplex, edgeVariables, cutEdges), 2));
			}
		}
	}

Complete Source

Just in case, right now, TspIpSolver should look something like this:
Show TspIpSolver

public class TspIpSolver<V,E> {
	
	public static enum Option{
		lazy,userCut, randomizedUserCut, christofidesApprox, christofidesHeuristic,twoOpt,incumbent;
	}
	
	private EnumSet<Option> options;
	private IloCplex cplex;
	private TspInstance<V,E> tspInstance;
	private final ImmutableBiMap<E,IloIntVar> edgeVariables;
	private ImmutableSet<E> edgesInOpt;
	private double optVal;
	private IloIntVar[] edgeVariablesAsArray;
	
	
	public TspIpSolver(TspInstance<V,E> tspInstance) throws IloException{
		this(tspInstance,EnumSet.of(Option.lazy, Option.userCut, Option.christofidesApprox, Option.christofidesHeuristic));
	}
	
	public TspIpSolver(TspInstance<V,E> tspInstance, EnumSet<Option> options) throws IloException{
		this.options = options;
		this.tspInstance = tspInstance;
		this.cplex = new IloCplex();
		UndirectedGraph<V,E> graph = tspInstance.getGraph(); //for convenience, we will be using this a lot
		this.edgeVariables = Util.makeBinaryVariables(cplex, graph.getEdges());
		edgeVariablesAsArray = edgeVariables.inverse().keySet().toArray(new IloIntVar[]{});
		//the degree constraints
		for(V vertex: graph.getVertices()){
			cplex.addEq(Util.integerSum(cplex, edgeVariables, 
					graph.getIncidentEdges(vertex)), 2);
		}
		//the objective
		cplex.addMinimize(Util.integerSum(
				cplex, edgeVariables, graph.getEdges(),tspInstance.getEdgeWeights()));
		if(options.contains(Option.lazy)){
			cplex.use(new IntegerCutCallback());
		}
		if(options.contains(Option.userCut)){
			cplex.use(new MinCutCallback());
		}
	}
	
	public void solve() throws IloException{
		if(!cplex.solve()){
			throw new RuntimeException();
		}
		optVal = cplex.getObjValue();
		edgesInOpt = ImmutableSet.copyOf(edgesUsed(cplex.getValues(edgeVariablesAsArray)));
		cplex.end();
	}
	
	public ImmutableSet<E> getEdgesInOpt(){
		return edgesInOpt;
	}
	
	public double getOptVal(){
		return optVal;
	}
	
	/**
	 * assumes  edgeVarVals[i] in {0,1}, up to some tolerance.  
	 * @param edgeVarVals
	 * @return the edges where the variable takes the value one.
	 */
	private Set<E> edgesUsed(double[] edgeVarVals){
		Set<E> ans = new HashSet<E>();
		for(int e = 0; e < edgeVarVals.length; e++){
	        if(Util.doubleToBoolean(edgeVarVals[e])){
	        	ans.add(edgeVariables.inverse().get(edgeVariablesAsArray[e]));
	        }
	    }
		return ans;
	}
	
	private Map<E,Double> getNonZeroEdgeWeights(double[] edgeValues){
		Map<E,Double> edgeWeights = new HashMap<E,Double>();		
		for(int i = 0; i < edgeValues.length; i++){
			if(edgeValues[i] > Util.epsilon){
				edgeWeights.put(edgeVariables.inverse().get(edgeVariablesAsArray[i]), edgeValues[i]);
			}
		}
		return edgeWeights;
	}
	
	private class IntegerCutCallback extends LazyConstraintCallback{
		
		private double minCutVal;
		
		public IntegerCutCallback(){
			minCutVal = 1.99;
		}

		@Override
		protected void main() throws IloException {
			Set<E> edgesUsed = edgesUsed(this.getValues(edgeVariablesAsArray));     
			Set<Set<V>> connectedComponents = tspInstance.getConnectedComponents(edgesUsed);
			if(connectedComponents.size() > 1){
				for(Set<V> connectedComponent: connectedComponents){
					this.add(cplex.ge(Util.integerSum(cplex, edgeVariables, tspInstance.cutEdges(connectedComponent)),2));
				}			
			}
		}			
	}
	
	private class MinCutCallback extends UserCutCallback{
		
		private double minCutVal;
		
		public MinCutCallback(){
			minCutVal = 1.99;
		}

		@Override
		protected void main() throws IloException {
			//do not attempt to add any cutset constraints until CPLEX is done adding constraints
			if(!this.isAfterCutLoop()){
				return;
			}
			double[] edgeVals = this.getValues(edgeVariablesAsArray);
			Map<E,Double> edgeWeights = getNonZeroEdgeWeights(edgeVals);
			UndirectedGraph<V,E> graph = tspInstance.getGraph();
			MinCutSolver<V,E> minCutSolver = new MinCutSolver<V,E>(graph,edgeWeights);
			Set<Set<E>> cutSets = new HashSet<Set<E>>();
			V source = graph.getVertices().iterator().next();
			for(V sink : graph.getVertices()){
				if(sink != source){
					Set<V> cutNodes = minCutSolver.computeMinCut(source, sink);
					Set<E> cutEdges = tspInstance.cutEdges(cutNodes);
					double cutVal = Util.calcSum(cutEdges,edgeWeights);
					if(cutVal < minCutVal){
						cutSets.add(cutEdges);
					}
				}
			}
			for(Set<E> cutEdges: cutSets){
				this.add(cplex.ge(Util.integerSum(cplex, edgeVariables, cutEdges), 2));
			}
		}
	}
}