Three to four weeks of statistical mechanics lectures are planned. Today there is a motivation and an introduction. There is a book that can serve as a resource. The author is McQuarrie and studying closely Chapters 1-6 and 11 is recommended.

Motivation

Statistical mechanics connects the microscopic to the macroscopic. It serves as a bridge between the two. Thermodynamics is blind to the microscopic world. For example, there are equations of state that are independent of atomistic interpretations.

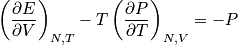
Thermodynamics does provide mathematical relations that are very useful, but they need experimental input. Once we know the equation of state, we can get much information, but thermodynamics does not provide microscopic intuition. Relations in thermodynamics give a little feeling but are not as intuitive as in statistical mechanics.

There is a need for experimental input when using thermodynamics. In contrast, experiments aren't needed when applying statistical mechanics. Assumptions about the system are made and information is plugged into the Schrodinger equation.

Summary

Advantages of thermodynamics

• Provides mathematical relations with experimental input
• independent of atomistic interpretations

Drawbacks of thermodynamics

• Need experimental input
• No physical intuition

Statistical mechanics

Statistical mechanics starts from microscopic world. Assumptions are made about particles, and the Schrodinger equation is applied. A solid contains

vibrating atoms. Assumptions are made about the interactions between particls and the heat capacity is derived. Statistical mechanics starts with quantum mechanics, which is plugged into the framework of statistical mechanics and connected to thermodynamics. Statistical mechanics provides an intuition about the system, and it is possible to get properties that may not have been as intuitive. It is possible to use statistical mechanics without experimental input.
The goal of statistical mechanics is to understand and predict macroscopic phenomena from microscopic interactions. This provides a more intuitive, mechanistic understanding of thermodynamic quantities. First-principles calculations are possible. These calculations, called ab initio calculations employ the Schrodinger equation to get properties. No experimental input is needed and parameters are not fitted to the solid. Probability theory is used in statistical mechanics.

Examples

An example of improving mechanistic understanding is a better physical interpretation of entropy. Entropy is a state function, is additive, and its maximum defines equilibrium, but what does it mean physically? The concept of entropy was introduced, but we hope to gain an intuitive understanding through statistical mechanics. Satistical mechanics says that entropy is a measure of disorder. Other examples of improved physical intuition include the meaning of the second and third law.

There are other examples of fruit generated by statistical mechanics. It is possible to derive the heat capacity by the way atoms interact. The form of the heat capacity as temperature goes to zero and its asymptotic nature is derived. This is not possible with classical mechanics.

Another example includes derived the typical topology of a phase diagram. Topology refers to the material being liquid at high temperature, a disordered solid at moderate temperature, and ordered at low temperature. Entropy, heat capacity, and phase diagrams are all explained more intuitivelly and more mechanistically.

The ideal gas equation of state is derived from first principles caculations. Particles in a gas are assumed not to interact. It is possible to get explicit expressions for chemical potential depending on assumptions of interactions. A limitation of first-principles calculations is that the Schrodinger equation must be applied to more complicated systems.

A more complicated example of first-principles calculations is research of the lecturer. The lattice dynamics and thermodynamic properties of the \beta-Sn phase were calculated. Every atom can vibrate, and there need to be assumptions about the vibrations. With an interaction model, it is possible to derive thermodynamic properties. One assumption is that they vibrate independently. With correct assumptions, the experiments and calculations can match perfectly. The phase diagram can be derived, and it is possible to get information about entropy and volume.

Consider the different degrees of freedom in a system of CdMg. The configurational degrees of freedom are related to the ways to place atoms. This is the largest contribution. From this it is possible to derive the correct order in phase diagrams. Consider other degrees of freedom which can be decoupled from each other.

Summary

• Statistical mechanics starts from microscopic world
• Solid vibrating atoms --> interactions --> derive heat capacity

Has the goal of understanding and predicting macroscopic thermodynamic phenomena from microscopic interactions

• more intuitive mechanistics understanding
• enable first principle predictions (no experimental input)

Typical topology of a phase diagram: we are going to understand through entropy why the phase diagram looks the way it does

• Liq at high T, disordered solution at intermediate T, ordred at low T

Deriving the ideal gas law

• assuming no interactions
• chemical potential with explicit form for

Silicon vibrational properties from interaction model + stat mech + thermo

Introduction to Statistical Mechanics

We are going to use Schrodinger's equation. Think now from a classical point of view. The properties and equation of state are from V, N,and T. It is macroscopically simple. But microscopically we are dealing with

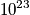
particles that move with some velocity. Each particle moves with some velocity, and there are position and momentum vectors associated with each particle.

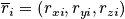
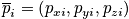
The vectors are of dimension

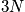
, and there is enormous complexity. The time dependence of these vectors are given by Newton's equation of motion for some given boundary condition. One condition is the energy.

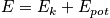
Quantum mechanically, everything is gained from the wave function, including the state of the system. The wavefunction is below

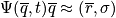
Consider the many body Schrodinger equation. Assume stationary conditions and solve the eigenvalue problem to find eigenvalues and eigenstates.

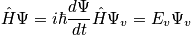
There are rapid fluctuations between states. Classically and quantum mechanically, there are a huge number of degrees of freedom, and the first postulate resolves this problem.

Summary

With a gas, we get the thermodynamics properties from its equations of state

In a classical description each particle has a position

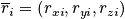
and momentum

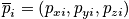
• Two vectors with dimension 3N

The time depenence of these vectors are given by Newton's equation of motion, for certain boundary condition

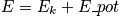
Quantum mechanically, the state of the system is given by

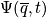
where

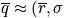
from

, (

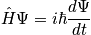
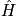
is Hamiltonian) Stationary conditions lead to

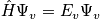
The grand idea behind statistical mechanics

Observation time over which therodynamic quantities are mesured is very large compared to the time scale of molecular activity. Consider the momentum evolution as a function of time. The system does fluctuate but is near equilibrium. The average is a good description. The fluctuations are not seen at time scale

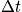
. Over

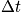
the particle has accessed many states. Much of phase space has been covered, and value of momentum is close to some average number.

Thermodynamic properties are time averages of microscopic counterparts. There is a crucial connection between microscopic states and thermodynamics. Consider the thermodynamic energy,

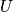
. Write the energy explicitly through a classical description and quantum description.

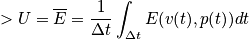
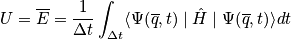
It is not easy to calculate the time dependence and practically impossible to calculate the time evolution of a quatum mechanical system or an N-body system. The major postulate of quantum mechanics connects time averages with something we can compute.

The time average is equal to the weighted average over all possible states a system can lie in for a given boundary condition. The average energy can be written as a weighted average over states. Associate each energy with a probability that the system is at that energy.

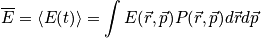
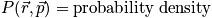
The probability density is still a hard function of position and momentum

Summary

Observation time over which therodynamic quantities are mesured is very large compared to the time scale of molecular activity

• we take the average over time
• the crucial connection between micorscopic states and thermo

Thermodynamic properties are time averages of their microscopic counterparts

Classical description:

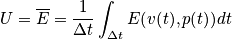
Quantum description:

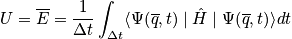
It is practically impossible to calculate the time evolution of an N-body system!

Time average = weighted average over all possible states that a system can be in (for a given boundary condition)

Classical:

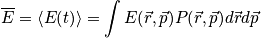
where

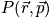
is the probability density.

Major postulate of statistical mechanics

Sum over all states. Multiply by the energy of a state and probability of being in that state. Sum over all states to calculate the expected value of energy. This is done instead of solving Newton's equation of motion or time averaging. Given

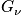
we can calculate everything.

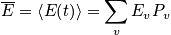
Go after the probability function. Plug in, and get average quantities. Get values from first principles.

Summary

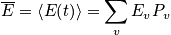
With

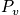
(the probability function), we can calculate everthing!

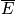
can be plugged into thermodynamic equations.

Simple Example

Calculate the average number of students asleep given it is Wednesday morning and a particular lecturer is teaching. This is a function of time. Consider the state of each student. The probability is given below in a time dependent equation and in an equation given by approximating with an average quantity,

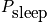
, which is the average probability of falling asleep at any time.

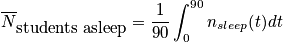
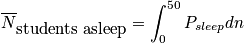
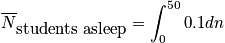
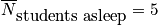
In statistical mechanics, there is a gamble that there is a good average number. In a wildly flutuating system, such as with a change in teacher, the boundary conditions change, and the probability would also change. Stationary conditions are assumed, and

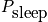
is a very simple example.

It is possible to take a snapshot and work backwards to estimate probability.

Summary

Let's say we want to calculate average number of students asleep, given the boundary condition that it is a 90 minute class.

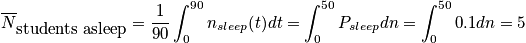
where

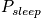
is the average probability for being in a sleep stateClosing RemarksThere are two ways to remove time dependence that are not connected.

A review of quantum mechanics is next. Slides were shown in lecture, and below are a few remarksMechanical system is determined by a wavefunction

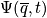
. Energy takes on discret values
Degeneracy is common. There are many

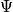
with same

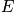
• Calculations are much easier in many-body problems when the Hamiltonian is summed up and some interactions are assumed to be de-coupled. When decoupled, the energy becomes a sum over particle energies.