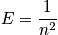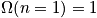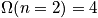There is real statistical mechanics today. An ensemble is defined and an average calculated.
Microcanonical & Canonical Ensembles
It has been demonstrated that there is a huge number of microstates. It is possible to connect thermodynamics with the complexity of the microscopic world. Below are definitions.
Microstate
A microstate is a particular state of a system specified at the atomic level. This could be described by the many-body wavefunction. A system is something that over time fluctuates between different microstates. An example includes the gas from last time. There is immense complexity. Fix the variables <math>T, V,</math> and <math>N</math>. With only these variables known, there is no idea what microstate the system is in at the many body wavefunction level.
Consider a solid. It is possible to access different configurational states, and two are shown below. Diffusion is a process that results in changes in state over time. X-ray images may not be clear due to the diffusion of atoms and systems accessing different microstates. There may be vibrational excitations, and electronic excitations correspond to the excitation of electrons to different levels. These excitations specify what state the solid is in. Any combination of excitations specify the microstate of a system.
Summary
A particular state of a system specified at the atomic level (many function wavebody level
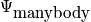
. The system over time fluctuates betwen different microstates
- There is immense complexity in a gas
- Solid
- Configurational states
- Vibrational excitations
- electronic excitations
- There is usually a combination of these excitations, which results in immense complexity
- Excitations specify the microstate of the system
Why Ensembles?
A goal is to find
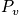
. Thermodynamic variables are time averages. Sum over the state using the schrodinger equation to find energy and multiplying by probability. To facilitate averages, ensembles are introduced. Ensembles are collections of systems. Each is very large, and they are macroscopically identical. Look at the whole and see what states the system could be in. Below is a diagram of systems and ensembles. Each box represents a system, and the collection of systems is an ensemble. Each box could represent the class, and v could represent the sleep state. Look at the properties of the ensemble. There are
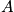
;macroscopically identical systems. Eventually
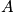
is taken to go to
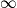
. Each system evolves over time.
Deriving P_v
The probability,
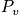
is defined for different kinds of boundary conditions. When looking at the probability that students in a class are asleep, it is possible to take an instantaneous snapshot. The term
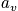
is the occupation number and is defined as the number of systems that are in the state
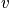
at the time of the snapshot. The fraction of systems in state
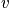
is
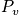
. This is one approximation to get the probability, and it could be a bad approximation.
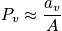
There are an additional definitions of
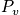
. It is equal to the probability of finding a system in state v at time t or identically it is the fraction of time spent by the system in state v. In the case of the sleep example, it is equal to the fraction of time that any one is in the sleep state.
The time average corresponds to looking at a class and seeing for what fraction of time does it find someone in the class asleep. The ensemble average corresponds to looking at the set of identical classes and seeing how many classes have at least one student asleep. There is a correlation between the state average and the time average. There is a need of boundary conditions. Take a picture of a large number of systems, look at everyone, and average.
Summary
Recap:
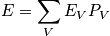
To facilitate averages, we introduce "ensembles" that we average over
- Averaging over many bodies rather than averaging over time
- Example: student = system, v =sleepstate
Ensemble of systems:
- 'A' (a very large number) macroscopically identical systems
- Each system evolves over time
Probability:
- Take an instantaneous snapshot
- Define
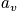 = #of systems that are in state v at the time of snapshot
= #of systems that are in state v at the time of snapshot - Fraction of systems in state v is
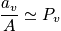
- Probability to find a system in statevat timet
- Fraction of time spent in statev
Microcanonical Ensemble
The boundary conditions of all systems of the microcanonical ensemble are the same. The variablesN, V,andEcannot fluctuate. Each system can only fluctuate between states with fixed energy,E.
It is possible to get degeneracy from the Shrodinger equation.
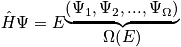
Consider the example of the hydrogen atom. Below is an expression of the energy proportionality and the degeneracy when
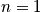
and
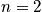
<P> </P>
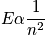
<P> </P>
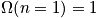
<P> </P>
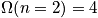
What is Pv in microcanonical ensemble?
All states should be equally probable with variables
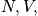
and
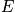
[ fixed. The term
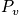
is the probability of being in any
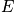
state for a system, and it should be equal to a constant. An expression is below. Each state can be accessed, and one is not more favored. This is related to the principle of a priori probability. There is no information that states should be accessed with different probability.
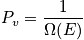
Example
Consider an example of a box and gas. All the atoms are in one corner in the second box. Add to get complete degeneracy. The value of
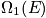
is large; there is enormous degeneracy.
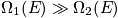
Consider a poker hand. There is a lot of equivalence in bad hands. These are dealt most of the time and correspond to
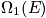
. The royal flush corresponds to
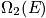
. It is equally probable, but there are many fewer ways to get the royal flush. There are the same boundary conditions. In an isolated system, in which
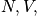
and
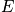
are fixed, it is equally probable to be in any of its
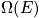
possible quantum states.
Summary
The variables
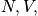
and
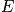
are fixed
- Each system can only fluctuate between states with fixed energy
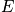 (like from Schrodinger's equation)
(like from Schrodinger's equation) -
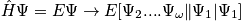
-
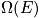
- All states are equally probable, and are given equal weight.
Hydrogen atom
Probability of being in any E state for a system
- employed the principle of equal a priory probabilities
-
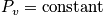
-
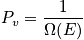
Systems
- Equally more probable
- Some accessed more times because of large degeneracy number
- There's just a lot more ways to get configuration left (like a craphand) than the right (like a straight flush)
-
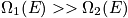
An isolated system (
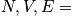
fixed) is equally probable to be in any of its
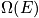
possible quantum states.
Canonical Ensemble
There is a different set of boundary conditions in the canonical ensemble. There are heat conducting walls or boundaries of each system. Each of the
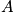
members of the ensemble find themselves in the heat bath formed by the

members. Each system can fluctuate between different microstates. An energy far from average is unlikely. In the picture below, the energy of the ensemble on the right side of the ensemble is fixed, while the energy of a particular system is not fixed and can fluctuate.
Take another snapshot. There is interest in the distribution. The term
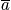
is equal to the number of systems in state
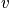
.
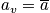
Below is a table of microstates, energy, and occurence, and a graph. In the graph, equilibrium has occurred, but all states can be accessed. It is possible to access different states some distance from the average energy. The total energy,

, is fixed and is equal to the integral of the curve. As the number of systems increases, the curve becomes sharper.
 |
1 |
2 |
3 |
 |
|---|---|---|---|---|
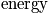 |
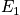 |
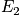 |
 |
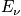 |
 |
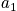 |
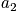 |
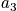 |
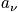 |
Constraints
Below are constraints. The first is the sum of the occupation number. The second constraint is possible due to the system being isolated.
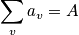
<P> </P>
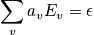
The term
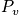
is the probability of finding the system in state
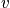
. It is possible to use snapshot probability. There are many distributions that satisfy the boundary conditions. There is a better way to find
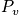
, and a relation is below. It corresponds to the average distribution. This is associated with a crucial insight.
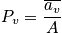
Crucial Insight
An assumption is that the entire canonical ensemble is isolated. No energy can escape, and the energy

is constant. Every distribution of
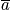
that satisfies the boundary conditions is equally probable. it is possible to write many body wavefunction because the energy of the entire ensemble is fixed. The principle of equal a priori probabilities is applied. Look at the whole distribution that satisfies the boundarty condition. Each distribution of occurance numbers must be given equal weights.
Summary
The variables
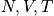
are fixed
- There are heat conducting bondaries of each system
- Each of the
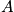 (= large number) members finds itself in a heat bath, formed by the
(= large number) members finds itself in a heat bath, formed by the
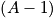 other members
other members - Take snapshot; get distribution
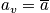 (= # of systems in state
(= # of systems in state
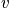 )
)
Constraints
The total energy,

, is fixed
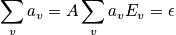
(isolated!)
Probability
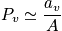
is an approximation.
- Better to use
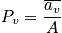 , the averaged distribution
, the averaged distribution - There is an assumption that the whole canonical ensemble is isolated and that energy
 is constant. Every distribution of
is constant. Every distribution of
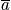 that satisfies the boundary conditions is equally probable.
that satisfies the boundary conditions is equally probable. - We are applying the principle of equal a priori probabilities, and each distribution of occurance numbers must be given equal weights.
Some Math
Consider every possible distribution consistent with boundary conditions, and for each distribution consider every possible permutation. The term
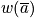
is equal to the number of ways to obtain a distribution
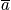
, where

is the number of systems in state
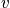
. A bad hand in poker is defined by a large number of
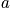
. Use the multinomial distribution.
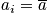
<P> </P>
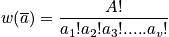
<P> </P>
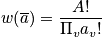
<P> </P>
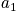
<P> </P>
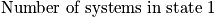
<P> </P>
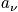
<P> </P>
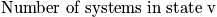
Below are expressions of the probability to be in a certain state. The term
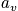
is averaged over all possible distributions. Every distribution is given equal weight, and the one with the most permutations is the most favored.
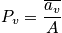
<P> </P>
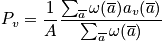
Example
Below is an example of four systems in an ensemble. The term
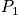
is the probability of any system to be in state
.
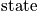 |
 |
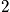 |
|---|---|---|
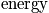 |
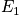 |
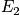 |
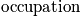 |
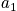 |
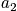 |
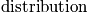 |
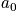 |
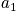 |
<P> </P>
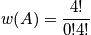
<P> </P>
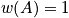
<P> </P>
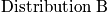
<P> </P>
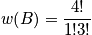
<P> </P>
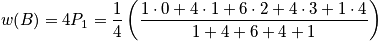
<P> </P>
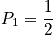
<P> </P>
Distribution of
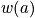
The term
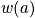
is the number of permutations for a particular distribution. As the number of systems increases, or asAincreases, the distribution becomes more peaked.
Consider the probability.
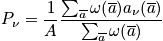
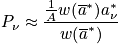
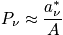
(Equation 1)
Look at the distribution that maximizes
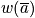
, the permutation number. To get
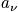
, maximize
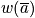
subject to the constraints below.
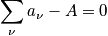
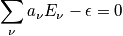
Use Lagrange multipliers, and maximize
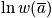
in order to be able to use Stirling's approximation.
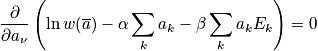
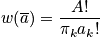
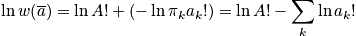
Use Stirling's approximation as
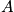
and the occupation number,
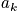
, go to infinity.
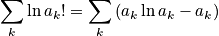
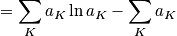
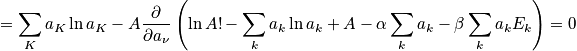
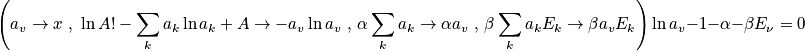
[
The term
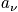
is the occupation number that maximizes the expressione
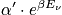
, where
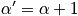
. Use constraints to determine the Lagrange multipliers and determine the probability.
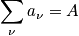
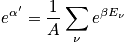
The probability of being in a certain state
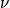
can be calculated, and it is still in terms of the second Lagrange multiplier. Plugging back into Equation 1:
Partition Function
The denominator is the partition function,
. It tells us how many states are accessible by the system. Determine
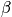
, a measure of thermally accessible states . Look at how the partition function connects to macroscopic thermodynamic variables. Find
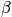
and find
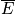
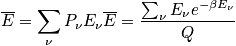
Consider the average pressure. The pressure for one microstate is
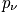
.
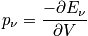
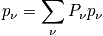
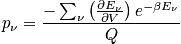
Summary
In the case of a canonical ensemble, the energy of the entire ensemble is fixed. Each state is equally probable, and there is degeneracy. The probability is a function of how many ways to get the distribution. The distribution with the most permutation is the most probable. The graph can become very peaked. Once the distribution is known, do a maximization of
. Use Lagrange multipliers and two constraints. The term
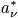
is the distribution that maximizes an expression. This is what is most often found. Go back to the probability, get an expression, and give part of it a name. The term
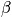
is a measure of how many states are thermally accessible.
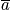
Consider every possible distribution
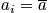
(consistent with boundary conditions)
- For each distribution, consider every possible permutation
- The number of ways to obtain
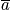 is
is
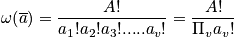 , where
, where
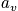 is the number of systems in state
is the number of systems in state
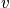 .
.
Probability
Averaging
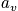
over all possible distributions.
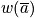
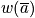
is very peaked around a specific distribution
Increase
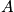
and
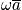
becomes more peaked
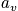
To get
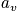
, maximize
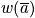
subject to constraints.
Find the partition function,