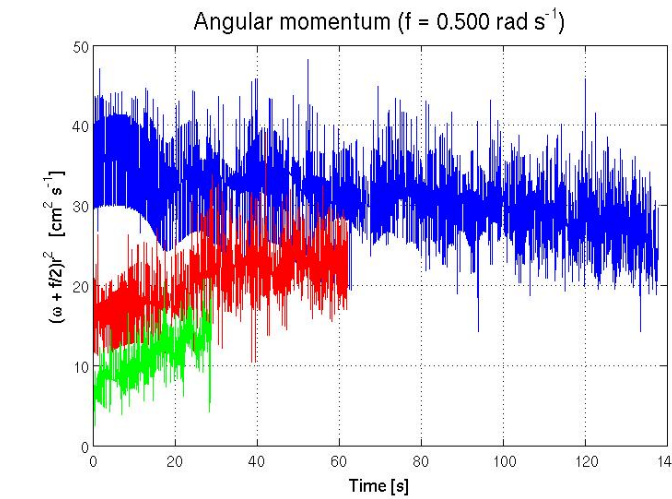
This image displays the evolution of (w+f/2)r^2 for an experiment with f = 0.500 rad/s. w is the angular velocity of a particle in the rotating frame of reference, f is the Coriolis parameter, and r is the distance of the particle from the rotation axis. This quantity is proportional to the angular momentum and should remain constant if a) the angular momentum is conserved and b) the particles are in fact tracers of the angular momentum-conserving flow.
Angular momentum conservation is clearly not perfectly satisfied, with two particles actually increasing their angular momenta for unknown reasons. However, the changes in angular momentum experienced by an individual particle over the course of the experiment are generally smaller than the differences in angular momenta between particles. Thus the particles can be reasonably said to have distinct values of angular momentum.
Contrary to some prior claims, the angular momentum of every water parcel is not equal to the angular momentum of a water parcel with w = 0 located at the outer edge of the water tank. This is because when the experiment begins from solid body rotation, all water parcels have w = 0 but they are not all at the outer edge of the water tank. If the fluid is assumed to be invisicid and axisymmetric, then there is no way to generate the torques necessary to change the angular momentum. Thus each water parcel retains its initial angular momentum.
Parcels with different initial radii should retain different angular momenta as they flow in towards the drain. The fact that the water parcels have different angular momenta is thus evidence that the angular momentum of any given water parcel CANNOT be identified as the angular momentum of a nonmoving (in the rotating frame of reference) parcel at the outer edge of the tank.
Two caveats must be noted for this image. First, because water is flowing out of the tank the values of r used to calculate (w+f/2)r^2 must be corrected to take account of the recession of the water surface from the camera. If the particle tracker effectively measures angular distance of a particle from the rotation axis, then the angular distance can decline solely by having the water surface move down (particle move away from the camera) without any real reduction in r. This effect is potentially significant because of the squaring of r. Without the correction, a 10% increase in the distance of the water surface from the camera could thus bring about an underestimate of the angular momentum of up to about 20%.
The correction for the changing water depth was applied by assuming that an initial depth of ~20 cm dropped to zero linearly over the full time for which particle tracks were recorded (probably about twice as long as shown in the figure). However the results presented above are insensitive to the choice of (plausible) assumptions about the tank draining rate.
Second, comparison of particle trajectories with the transport of dye by the flow in a similar balanced flow experiment suggests that the surface particles used for tracking may not in fact be advected along with water parcels in the body of the flow. Thus it is somewhat unclear whether the angular momentum of the trackable surface particles is actually a quantity of physical relevance to the flow.
These ideas are expanded upon more quantitatively and at greater length in a relevant lab report available here.
Todd Mooring
mooring11@gmail.com
21 May 2011