Photo by Keith Finlay, courtesy of Wikimedia Commons |
Part A
Velodromes are indoor facilities for bicycle racing. Olympic velodromes are usually ovals 250 m in circumference with turns of radius 25 m. The peak banking in the turns is about 42°. Assuming a racer goes through the turn in such a velodrome at the optimal speed so that no friction is required to complete the turn, how fast is the racer moving?
System:
The rider will be treated as a point particle.
Interactions:
The rider is subject to external influence from the earth (gravity) and from the track (normal force). We assume friction is not present, since we are told to determine the speed at which friction is unnecessary to complete the turn.
Model:
Point Particle Dynamics and Uniform Circular Motion.
Approach:
Diagrammatic Representation
Since we are assuming no friction is needed, we have the free body diagram and coordinate system shown above.
Mathematical Representation
The corresponding equations of Newton's Second Law are:
Notice that we have used a true vertical y-axis and true horizontal x-axis. The reason will become clear in a moment.
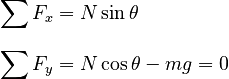
The vertical forces cancel out, but the resultant force in the x-direction is not zero
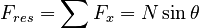
This force is directed horizontally inwards toward the center of the curve, causing the bicycle to move in a horizontal circle. We therefore set this resultant Force equal to the force needed to keep the bicycle of mass m moving in a circle of radius r
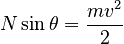
The situation here is very different than that of an object sliding down an inclined plane. In the case of an object moving along the plane, the acceleration will have both x and y components if our untilted coordinates are used. For an object moving along a banked curve, the object will not be moving up or down and so ay must be zero. The x-component of the acceleration will of course not be zero because the object is following the curve. This difference between motion along a banked curve and motion down an inclined plane is the reason we use tilted coordinates for the incline and traditional coordinates for the curve.
It is not appropriate to assume N = mg cosθ. Note that we have not tilted our coordinates to align the x-axis with the ramp. Thus, the y-direction is not perpendicular to the ramp.
From the y-component equation, we find:
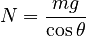
Note both the similarity to the standard inclined plane formula and the important difference.
Substituting into the x-component equation then gives:
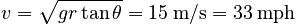
Is this speed reasonable for a bike race?
Note that our result is independent of the mass of the rider. This is important, since otherwise it would be impractical to construct banked curves. Different people would require different bankings!
Photo courtesy Wikimedia Commons, uploaded by user The359. |
Part B
The Indianapolis Motor Speedway (site of the Indianapolis 500 race) has four turns that are each 0.25 miles long and banked at 9.2°. Supposing that each turn is 1/4 of a perfect circle, what is the minimum coefficient of friction necessary to keep an IndyCar traveling through the turn at 150 mph from skidding out of the turn?
System:
The car plus contents will be treated as a point particle.
Interactions:
The car will be subject to external influences from the earth (gravity) and from the track (normal force and friction).
Model:
Point Particle Dynamics and Uniform Circular Motion.
Approach:
Diagrammatic Representation
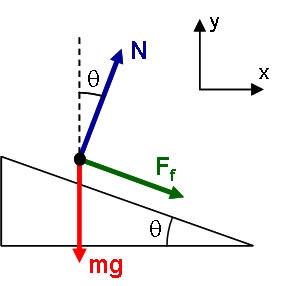
The free body diagram from Part A is modified to include friction, as shown above.
In this problem, it is not clear a priori which way friction should point. Under certain conditons friction will point up the incline while in others it will point down (can you describe the conditions for each case?). This ambiguity should not prevent you from solving. Simply guess a direction. If you guess wrong, your answer will come out negative which will indicate the correct direction.
Mathematical Representation
The resulting form of Newton's Second Law is:
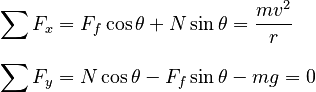
We have three unknowns (N, Ff, and m) but only two equations. To solve, we must develop another constraint. To do so, we must notice a key phrase in the problem statement. We are asked to find the minimum coefficient of friction. The minimum coefficient will be the value such that the static friction force is maximized, satisfying:
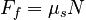
Remember that the point of contact of tires with the road surface is static (unless the car is in a skid) so static friction applies here. That is the reason that there is a minimum coefficient.
Whenever static friction applies, it is important to justify using the equation Ff = μN, since it is also possible that Ff < μN.
With this substitution, we have:
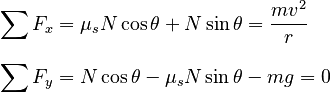
Proceeding as in Part A:
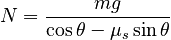
which is then substituted into the y-component equation to give:
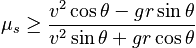
The substitutions here require some thought. The turns are quarter-circle segments with a length of a quarter mile each. Thus, they have the same radius of curvature as a full circle with circumference 1 mile. The corresponding radius is 256 meters. Then, converting the speed to m/s and using the formula derived above gives:
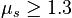
Given our answer to Part A, we expect that μs can be as small as zero if v2 = gr tanθ. Is that fact reflected in our formula?
Our answer is slightly in error. The normal force exerted on the car is actually increased beyond our assumed value by the presence of airfoils at the front and back of the car that generate negative lift (a downward force, often simply called "downforce"). This force is specifically intended to increase the maximum friction force available from the tires. As a result, the friction coefficient can likely be lower than our answer and still keep the car on the track. How large (as a fraction of the car's weight) would the downforce have to be keep the minimum acceptable coefficient of friction below 1.0? Assume the downforce presses straight into the surface of the track. (IndyCars can generate more than three times their weight in downforce when traveling near top speed.)




1 Comment
Anonymous
You should discuss why you pick the coord system with horizontal rather than with x parrel to the plane.
DO NOT say things like "We therefore set this resultant Force equal to the force needed to keep the bicycle of mass m moving in a circle of radius r" because this suggests there is a centripetal force.
The idea is that DYNAMICS is F = ma and these are two different quantities. Becasue it is going in a circle it has acceleration v2/R to the center of circle (NOT parallel to plane). Simple eqns since then a is along one axis. But have to find N from y eqn, then v from x.
Actually simpler Eqns if you use coord syst along plane. Then x-Eq does not involve N and the result follows from x-component of accel.