 |
(Photo by the Forest Service of the U.S. Department of Agriculture.) |
According to the U.S. Forest Service1, dwarf mistletoe is a parasitic plant that grows on the branches of pine trees. The mistletoe extracts its water and nutrients directly from the tree. One rare aspect of dwarf mistletoe is its seed dispersal mechanism. Rather than relying on birds or wind to spread seeds from pine tree to pine tree, mature mistletoe fruit literally explodes (as a result of extreme water pressure within the fruit). The explosion hurles the seed away from the pine tree. The seeds are coated with a sticky substance which causes them to adhere to whatever they hit. Ideally, the seed hits another nearby pine tree and begins to sprout.
The seed dispersal mechanism has been studied by T.E. Hinds and F.G. Hawksworth2 using high-speed photography. They find that Arceuthobium cyanocarpum (the variety shown in the picture above) ejects its seeds with a speed of about 2100 cm/s.
Suppose that a certain dwarf mistletoe fruit expels a seed with a velocity of 2100 cm/s directed at 30° above the horizontal. Suppose further that the seed hits another tree at exactly the same height that it was launched from. Neglecting air resistance (note: neglecting air resistance is a poor assumption in this case) how far horizontally is the landing site displaced from the launch site?
1 Taylor, Jane E. and Mathiason, Robert L. "Limber Pine Dwarf Mistletoe", Forest Insect and Disease Leaflet 171. U.S. Dept. of Agriculture, Forest Service, 1999.
2 Science, Vol. 148, No. 3669 (Apr. 23 1965), pp. 517-519
Solution
System:
The seed is treated as a point particle.
Interactions:
Constant external force from the earth's (gravity (near-earth)).
Models:
Projectile motion, assuming One-Dimensional Motion with Constant Velocity in the horizontal direction and One-Dimensional Motion with Constant Acceleration in the vertical direction.
Approach:
Diagrammatic Representation
We first sketch the situation and define a coordinate system with acceleration only along the (negative) y-axis..

We choose the launch point to have the coordinates x = 0 m, y = 0 m and we choose to make t = 0 s at the instant of launch. We are now almost ready to summarize our givens, but we first have to deal with the velocity. When putting the information given in the problem into a form suitable for use in our equations, we must break up all vector quantities into their x and y components. For the initial velocity, this is done by constructing a vector triangle:
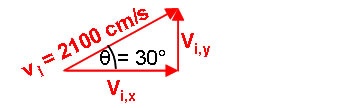
Using this triangle, we can see that:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {x}
= v \cos \theta = \mbox
Unknown macro: {18.2 m/s}
][ v_{y,{\rm i}} = v \sin \theta = \mbox
Unknown macro: {10.5 m/s}
]\end
Mathematical Representation
We can now state our givens:
Unknown macro: {latex} \begin
Unknown macro: {large} [ t_
Unknown macro: {rm i} = \mbox
Unknown macro: {0 s}
][x_
= \mbox
Unknown macro: {0 m} ] [y_
Unknown macro: {rm i}
= \mbox
][y = \mbox
Unknown macro: {0 m}
][ v_
Unknown macro: {x}
= \mbox
Unknown macro: {18.2 m/s}
] [ v_{y,{\rm i}} = \mbox
Unknown macro: {10.5 m/s}
][a_
Unknown macro: {y}
= -\mbox
Unknown macro: {9.8 m/s}
^
Unknown macro: {2}
]\end
Our end goal is to determine x, which will tell us the horizontal displacement of the seed during its flight. As usual, however, we must first find the time by using the y direction. The most direct approach is to use the Law of Change to find the time when the projectile returns to height y=0:
Unknown macro: {latex} \begin
Unknown macro: {large} [ y(t) = y_
Unknown macro: {rm i} + v_{y,{\rm i}} (t-t_
) + \frac
Unknown macro: {1}
Unknown macro: {2} a_
Unknown macro: {y}
(t-t_
Unknown macro: {rm i}
)^
] \end
which, after substituting
Unknown macro: {latex} $y(t_R) = 0$
, can be solved to give:
Unknown macro: {latex} \begin
Unknown macro: {large} [ t_
Unknown macro: {R}
= \mbox
Unknown macro: {0 s}
\qquad \mbox
Unknown macro: {or}
\qquad t_R = -\frac{2 v_{y}}{a_{y}} = \mbox
Unknown macro: {2.14 s}
] \end
We can now solve the x direction Law of Change:
Unknown macro: {latex} \begin
Unknown macro: {large} [ x(t_R) = x_
Unknown macro: {rm i} + v_
Unknown macro: {x}
(t-t_
) = -\frac{2 v_
Unknown macro: {x}
v_{y}}{a_{y}} = \mbox
Unknown macro: {39 m}
] \end
Follow Up
The Range Formula
Suppose that instead of calculating vx and vy explicitly to find our givens, we had just substituted the expressions v cosθ for vx and v sinθ for vy. You can check that the answer we found could have been written:
Unknown macro: {latex} \begin
Unknown macro: {large} [ x = -\frac{2 v^
Unknown macro: {2} \cos\theta \: \sin\theta}{a_{y}} = \frac{2 v^
\cos\theta \: \sin\theta}
Unknown macro: {g}
]\end
By using the trig identities for the sine of a sum, you can show that this becomes:
Unknown macro: {latex} \begin
Unknown macro: {large} [ x = \frac{v^
Unknown macro: {2}
\sin(2\theta)}
Unknown macro: {g}
] \end
This simple result is sometimes called the range formula. Remember how it is obtained: find the time until the projectile hits the ground from the y-motion; then find the x-position at that time.
You can use this range formula to prove two standard claims about projectiles fired over level ground:
- The range of projectiles fired with the same speed at complimentary angles (θ and 90°-θ) will be the same.
- The range of a projectile will be maximized when the launch angle is 45°, assuming the launch speed is independent of angle.


