Mass on a frictionless surface between two springs |
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representation
The mass m is subjected to force from the springs on each side. If you assume that the springs are in their relaxed state when the mass is at rest between them, then displacement of the mass to the right (as shown) compresses the spring on the right and extends the spring on the left. this results in restoring force to the left from both springs.
Mathematical Representation
Displacing the mass a distance x to the right results in restoring force from both springs. The spring to the right is compressed while the spring on the left is extended. The force from the spring on the right will be -kx (assuming, as we have, that the spring is at its neutral position, neither compressed nor extended, at the start). The force from the spring on the left will also be -kx, and will be in the same direction as the force from the first spring. The sum of these two forces is -2kx. Equating this to the force on the mass, which is equal to the mass times the acceleration, gives us the equation:
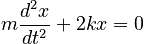
This is the familiar equation of simple harmonic motion (although the multiplier for x is now 2k instead of the usual k, because there are two springs). This has the solution:
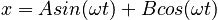
where:
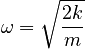
and A and B are determined by the initial conditions, the initial position xi and the initial velocity vi
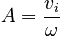
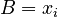
We have assumed above for simplicity that the springs are in their relaxed state when the mass is at x = 0, but this is not necessary. The springs can both be under tension or under compression. as long as they have not gone past their ranges of motion, the above expressions will still hold. Assume that each spring is compressed by the same amount Δ at the start. (Since the spring constants are equal, if the springs are not compressed by the same amount when first attached to the mass, they will automatically do so after you release them. The mass will settle into an equilibrium position that we will define as x = 0 )Now both springs are compressed by an amount Δ , and each therefore pushes with a force F = kΔ against both the wall and against the mass m. But since the Forces are of equal magnitude and opposite direction, the sum of the forces is zero, and the mass remains in its equilibrium position.
If we now displace mass m to the right by a distance x, we compress the spring more on that side, so the total force pushing to the left becomes Fleft = - k ( x + Δ ) , while we compress the spring on the left by a smaller amount (and possibly even extend it), so that the total force to the right becomes Fright = - k( - x - Δ ) . The total force is then
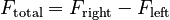
or
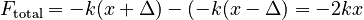
This is the same as before. The equation of motion is the same, and so the results will be the same. Note that all of this still holds if both springs are under tension instead of compression at the start.
Question
What would happen if we were to make the springs have different spring constants? Call them k1 and k2.
Answer
The mass will re-adjust to a new equilibrium position, where the compressions of the two springs are such that the forces from each spring are of equal magnitude and opposite direction. The restoring force of the system will be
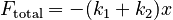
So you should replace 2k in the above expressions with ( k1 + k2 ) . This makes the frequency of oscillation
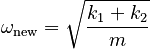
1 Comment
Anonymous
Isn't this problem missing a question?