The mathematical relationship between force and momentum, or, for systems with constant mass, the relationship between force and acceleration.
Motivation for Concept
When you push, kick or use some other means to apply force to an object, its velocity will change. It is of value to be able to quantitatively define the strength of such a push, kick or other force by examining the effects of the force on the object which is the target. Such a quantitative understanding of force is the basis of the science of dynamics.
Statement of the Law
Newton's Statement
"A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed." (The Principia by I. Newton, translated by I.B. Cohen and A. Whitman.)
Modern Statement
The modern form of the Law which is perhaps most consistent with Newton's statement is the integral formulation:
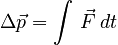
It is more common to express the Law in a differential form:
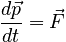
and, since it is rare to consider a system with changing mass, this form is often reduced to:
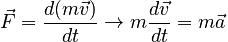
Use of the Law in Problem Solving
Form of the Second Law for Multiple Impressed Forces
When more than one force is impressed, the change in momentum is proportional to the vector sum of the forces. Thus, Newton's 2nd Law is usually expanded to state:
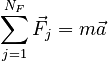
"Writing" Newton's Second Law
When a physics teacher or student says they are "writing Newton's 2nd Law" for a system, the form used should be that of the previous subsection, but expressed as several equations separated by vector component:
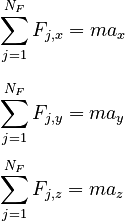
Directions that clearly have no forces acting are sometimes ignored.
Free Body Diagrams
Free body diagrams are pictorial guides to the specific form of Newton's 2nd Law for a given system. Drawing an accurate free body diagram shows visually what forces should be included in the statement of the law, and also gives information about the sign of the vector components of these forces.