A plot of position as a function of time is an often useful diagrammatic representation of kinematics problems.
Graphical Representation of Constant Velocity
Slope and Velocity
The mathematical definition of velocity is equivalent to the formula for the slope of a position versus time graph. To see the utility of this correspondence, consider the following position versus time graphs:
The first graph gives the position of some object (called object A) as a function of time. Looking at the graph, we can see that for each second of time that elapses, the object changes its position by 2 meters. This is the same as saying that the slope of the left plot is 2 m / (1 s) or, more simply, 2 m/s. Object A, then, is moving with a speed of 2 m/s.
In contrast, object B is only changing its position by 1 meter every second. Thus, it is moving with a speed of 1 m/s.
Finally, object C is changing its position by 2 meters every second, and so it has a speed of 2 m/s. Note that objects A and C have the same speed. The graphs are different, however, because object C is moving in the negative direction.
That doesn't necessarily mean objects A and C are moving in different actual directions. When looking at position as a function of time, we should always consider what coordinate system applies (does the positive x direction point east? west? north?...), and we haven't determined that for any of the graphs yet.
Intercept and Initial Position
Assuming the motion is defined to begin at t = 0, then the initial position of the motion (the position at time t = 0) can be found by taking the y-intercept of the position versus time graph. Thus, in the examples above, objects A and C begin thier motions at position x = 0, while object B begins its motion at position x = 5 m.
Graphical Representation of Constant Acceleration
Parabolic Form
From the formulas given in the model One-Dimensional Motion with Constant Acceleration, it is clear that a plot of position vs. time will give a parabola.
If the acceleration is positive the parabola will open upwards. The position at t = ti will be xi , as shown in the graph below (time at the origin is ti ):
|
In this case the position is positive. The fact that the plot of position vs. time is increased means that the initial velocity, vi , is also positive.
If the acceleration and the initial position xi were the same, but the initial velocity was negative , then the graph of position vs. time would look like this:
|
The parabola has a minimum value at the time tmin
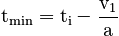
This information is intended to familiarize the reader with the shape of the curve and how it behaves. Obviously, if the object starts out at time t = ti its real motion will not be described by the portion of the curve for t < ti, and so an object moving with positive initial velocity and positive acceleration will not have such a "minimum" position - it will move in the same direction, with increasing speed, for all t > ti .
Concavity and Acceleration
Consider the position vs. time graph shown above. If you were to lay a ruler along the curve of the graph at the origin, the ruler would have to be horizontal to follow the curve, indicating zero slope. Thus, the velocity is zero at the origin. As you follow the curve, however, the ruler would have to be held at a steeper and steeper angle (see the lines added in the graph below). The slope grows with time, indicating that the velocity is becoming more and more positive (the speed is increasing). This positive change in velocity indicates a positive acceleration. In calculus terminology, we would say that a graph which is "concave up" or has positive curvature indicates a positive acceleration.
"Acceleration" versus "Deceleration"
In everyday speech, we distinguish between "accelerating" (speeding up) and "decelerating" (slowing down). In physics, both situations are referred to as acceleration (which can be confusing). It is possible to give an exact definition of deceleration, however. Deceleration occurs when the velocity and the acceleration vectors have opposite directions. "Acceleration" in the everyday sense (speeding up) occurs when the acceleration vector and the velocity vector have the same direction. The two cases can be distinguished graphically.
Graphs that Represent Speeding Up
|
|
positive acceleration |
negative acceleration |
|---|
Both the graphs that show "acceleration" in the everyday sense (speeding up) have slopes that are steepening with time. The only difference is that one of the graphs has a steepening positive slope and the other has a steepening negative slope.
Graphs that Represent Slowing Down
|
|
negative acceleration |
positive acceleration |
|---|
Both graphs showing "deceleration" (slowing down) have slopes that are approaching zero as time evolves. (Again, one has a negative slope and one has a positive slope.)
It is a very common misconception that a negative acceleration always slows down the object it acts upon. This is not true. It is important to note that a graph which has a negative slope approaching zero (slowing down) implies a positive acceleration, and a graph which has a negative slope that is steepening (speeding up) implies a negative acceleration. It may help you to remember that the concavity of the graph specifies the direction of the acceleration.









2 Comments
Anonymous
editorial comment: use of the word "obviously" serves the purpose of insulting the reader, risking support for their prior notions that they "cannot understand physics". I am specifically refering to the text near the parabolas.
perhaps presenting both parabolas with their left "arm" cut off (the more physical representation) and then ask: Why are the graphical reps of position vs. time cut off? This could be linked to a discussion somewhere of the physical meaning of time, as well as an operational definition of velocity and acceleration.
My preference is to lead instruction from the physics and not from the pure mathematics; helping early physics students make this difficult transition from where they are strong and fluent (mathematics) to the more abstract reps of real physical behavior.. as is referenced in motion diagrams etc.
Anonymous
Regarding the discussion about position vs. time grapns, with constant a, I thnm the discussion about "
.."The parabola has a minimum value at the time tmin ..."
Revision suggestion:
The moment of the minimum position is significant int that it is the turning point; when the objects motion reverses. The parabola has a minimum value at the time tmin....
Sara Jiulin