Subcritical manifolds and algebraic structures
In the morning we will go through the computation of symplectic cohomology for affine space. Using Cieliebak's result that subcritical Weinstein manifolds split, we'll obtain a computation for this class of manifolds.
- Compute the symplectic cohomology of the ball following the outline in Section (3f) of [Seidel]. The easiest way to do this is to follow the second approach, and compute the Conley-Zehnder index of the unique time-1 Hamiltonian orbit of the function
 when
when
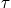 is not a multiple of
is not a multiple of
 .
. - Introduce the notion of a Weinstein manifold, and that of a subcritical Weinstein manifold. Explain Cieliebak's splitting result for subcritical manifolds (see Theorem 14.16 of [Cieliebak-Eliashberg]).
- Explain the statement of the main result of [Oancea-K]. Use this to compute symplectic cohomology for subcritical Weinstein manifolds.
In the afternoon, we will discuss algebraic structures on symplectic cohomology.
- Discuss the construction of operations on symplectic cohomology coming from moduli spaces of Riemann surface. Make sure to include a discussion of the BV operator. The construction of these operations is outlined in Section (8a) of [Seidel], which [Ritter] elaborates upon.
- Define the product on symplectic cohomology by counting pairs of pants. Explain the proof of associativity, and the construction of the unit.
- (Jo Nelson) Use the higher analogues, to define
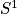 equivariant symplectic cohomology. Introduce contact homology, and outline the construction of an isomorphism between
equivariant symplectic cohomology. Introduce contact homology, and outline the construction of an isomorphism between
 equivariant symplectic cohomology and contact homology.
equivariant symplectic cohomology and contact homology.
1 Comment
Unknown User (jo_@mit.edu)
For #1: Alex Oancea computes the Conley-Zehnder index of the unique time-1 Hamiltonian orbit of the function relevant to computing SH of the ball in his survey paper in Section 3.2. http://arxiv.org/abs/math/0403377