Cotangent bundles and Viterbo Functoriality

In the morning, we will go through one method of computing the symplectic cohomology of cotangent bundles. 

1. Show that the unit cotangent bundle is a Liouville domain. Explain the correspondence between closed geodesics and Reeb orbits. State the isomorphism between symplectic cohomology and the homology of the free loop space (Theorem 3.5 in [Seidel]). Give the statement only with  coefficients.
2. Define the Morse homology of the free loop space following Section 2 of [Abbondandolo-Schwarz].
3. Explain the Abbondandolo-Schwarz construction of an isomorphism between symplectic cohomology and the homology of the free loop space, following Section 3 of [Abbondandolo-Schwarz]. Make sure to draw the pictures that are associated to these maps (i.e. counting pseudo-holomorphic half-cylinders in the cotangent bundle followed by gradient flow lines in the base).

In the afternoon,

1. Define the notion of a Liouville subdomain. Give examples coming from exact Lagrangian embeddings, and from Weinstein handle attachment.
2. Explain the construction of Section 2 in [Viterbo] associating maps on symplectic cohomology to Liouville subdomains. Warning: what Viterbo denotes 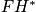  is the dual of the theory Seidel denotes  . To keep this talk consistent with the others, you should dualise Viterbo's statements.