1978 Silver Dollar Reverse |
A Coin rolling on its edge with a slight tilt will trace out a circle. What is its radius?
A coin is rolling without slipping on its edge, but tilts slightly to one side making an angle θ with the vertical, which makes the rolling path trace out a circle. What is the radius of this circle?
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representation
A coin rolling without slipping on a horizontal surface and tipped slightly at an angle θ to the vertical will roll in a circle of radius R. What determines this radius, and how does it vary with other characteristic values?
Call the radius of the coin r and its mass m. gravity (near-earth) pulls on the center of mass with gravitational force mg , and the surface the coin is rolling on pushes upwards with a normal force F. This must be equal to mg , since the coin neither rises nor falls above or below the surface.
We must choose a point about which to calculate the angular momentum and torque. A convenient spot is the point at which the coin touches the surface. Doing so allows us to neglect the normal force in our calculation of torque. We can also simply consider the rotation of the coin about that point in calculating the angular momentum (If we chose any other point, we'd have to consider the motion of the center of mass of the coin as well).
Mathematical Representation
The Moment of Inertia of the coin about its center (along an axis perpendicular to the coin's plane)is

We are interested in the Moment of Inertia about a point on the edge (although along a parallel Axis). We can easily determine this using the Parallel Axis Theorem :
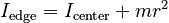
or

The angular rate of rotation about this point is the same as the angular rate of rotation about the center, ω. The angular momentum is thus
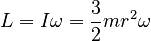
The direction of this angular momentum vecor will be pointing downwards at an angle θ with respect to the vertical, since the coin is tipped by that angle from the vertical:
The torque is due to the force of gravity acting on the center of mass of the coin (since there is no torque about the contact point due to the normal force, as the distance is zero)
The torque is given by
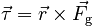
This has magnitude

This torque is equal to the rate of change of the angular momentum L with time, and the direction is horizontal (by the right-hand rule), which is perpendicular to the direction of the angular momentum. It therefore does not cause a change in the magnitude of the angular momentum, but only in its direction – it causes the angular momentum vector to rotate. The coin rolls in a circle.
This will not affect the vertical portion of the angular momentum, only the horizontal part, which has magnitude L cos(θ) , which will begin to rotate at angular velocity Ω :

Equating the extressions for the torque and inserting the value of the moment of inertia yields:
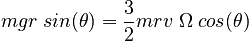
We can eliminate the precessional angular velocity Ω by observing that the speed of the coin must be given by

and hence Ω = ω (r/R) and

As in the case of the Spinning Top, this new rotational motion ought to contribute to the angular momentum of the system. in most cases of interest and practical importance, however, the small addition to the angular momentum this causes is negligible compared to the angular momentum of the coin rolling , and so it can be in the gyroscopic approximation, which holds that
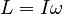
as long as

In this case that means that
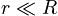
This is, in fact, the case – the coin rolls in a circle much large than its radius.
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>
