Moment of Inertia
A measure of the tendency of an object to maintain its rotational velocity about a specified axis of rotation. The moment of inertia depends linearly on the mass and quadratically on the distance of that mass from the axis of rotation. It plays the same role for rotational motion as mass plays for translational motion, being both the ratio of angular momentum to angular velocity and the ratio of torque to resultant angular acceleration, whereas mass is the ratio of (linear) momentum to velocity and the ratio of force to resultant linear acceleration.
Motivation for Concept
It is clear that some objects are more difficult to set into rotation or to stop from rotating than others. Consider four very different objects that are often rotated: a CD, a bicycle wheel, a merry-go-round in a park, and a carousel at an amusement park. Rotating a CD about its natural axis is trivial (simply brush it with your finger), and stopping its rotation is similarly trivial. Rotating a bicycle wheel is fairly easy (a push with your hand) and stopping its rotation is similarly straightforward. Rotating a park merry-go-round requires some effort (a full push with your legs) and stopping it takes some thought if you wish to avoid injury. Starting an amusement park carousel requires a large motor and stopping it requires sturdy brakes. These objects have distinctly different moments of inertia. Of course, they also have very different masses. Thus, mass is one factor that plays into moment of inertia.
Moment of inertia is not the same as mass, however, because it depends quadratically on size as well. This can be seen in a straightforward experiment. Find two boards that have the same weight but different lengths - for example a 1" X 2" board that is 12' long and a 2" by 4" board that is 3' long. Grab each by the center in each hand and rotate them. It will require dramatically more effort to rotate the longer board - 16 times as much, in fact. Note that the mass has not changed in this exercise, only the distance between the mass and the axis of rotation.
CD |
Bike Wheel |
Merry-Go-Round |
Carousel |
|---|---|---|---|
|
|
|
|
Photo courtesy Wikimedia Commons, |
Photo courtesy Wikimedia Commons, |
Photo by Eric Hart, courtesy Flickr. |
Photo courtesy Wikimedia Commons, |
Mathematical Definition
Rigid Body Simplification
For an introductory course, it is sufficient to consider the definition of the moment of inertia of a rigid body executing pure rotation (no translation relative to the axis) about a single axis of rotation. The importance of this statement is that every point in the body will maintain a fixed distance from the axis of rotation. This condition is specified so that the moment of inertia of the body remains constant.
Body as Sum of Point Particles
Under this condition, we can quickly derive the form and the utility of the moment of inertia by considering the rigid body to be a collection of Np point particles. Each of the Np point particles (of mass mi where i runs from 1 to Np) will obey Newton's 2nd Law:
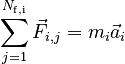
where Nf,i is the number of forces acting on the ith particle.
Cross Product with Radius
Taking the cross product of each side of this equation with respect to the radial distance from the axis of rotation:
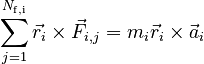
We can rewrite this using the definition of the angular acceleration and the torque:
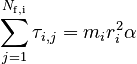
Note that for a rigid body that is undergoing pure rotation about a certain axis (recall our assumption), all particles will have the same angular acceleration.
Implementing a sum over the particles that make up the body then gives:
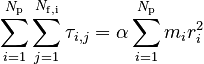
Moment of Inertia as Sum
The left side of this equation is simply the sum of all torques acting on the body. On the right side, we define the moment of inertia, I as:
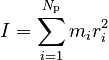
Uses of the Moment of Inertia
Role in Rotational Analog of Newton's 2nd Law
The work of the previous section allows us to write:
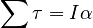
This is the rotational analog of Newton's 2nd Law, with the torque taking the place of the force, the angular acceleration taking the place of the (linear) acceleration and the moment of inertia taking the place of the mass.
Role in Angular Momentum
Under the assumption we discussed at the beginning of the derivation above, the moment of inertia is a constant. Thus, using the definition of angular acceleration, we can write:
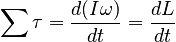
where, in the absence of a net torque, the quantity:
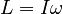
is conserved. By analogy with the linear case, we refer to L as the angular momentum of the rigid body about the specified axis.
Role in Rotational Kinetic Energy
We can similarly define a quantity analogous to the translational kinetic energy. We start with a relationship from angular kinematics:
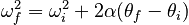
We then multiply by the moment of inertia to find:
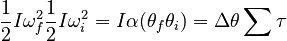
Noting the similarity to the Work-Kinetic Energy Theorem, and noting that each side has the units of Joules, a likely definition of rotational kinetic energy is:
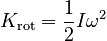
The consistency of this definition with the principle of conservation of energy can be seen in example problems like:
-
Down the Well — A mass falling while attached to a massive pulley.
-
Down the Ramp — Find the acceleration of a ball rolling without slipping on an inclined plane.
Summary of Analogies Between Mass and Moment of Inertia
This table presents a list of formulas in which moment of inertia plays a role in the angular formula analogous to that of mass in the linear formula.
Description |
Linear Formula |
Angular Formula |
|---|---|---|
Newton's 2nd Law / Angular Version |
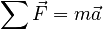 |
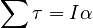 |
Momentum / Angular Momentum |
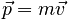 |
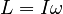 |
Kinetic Energy / Rotational Kinetic Energy |
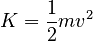 |
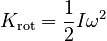 |
Calculating Moment of Inertia
Integrals in Cylindrical Coordinates
For continuous objects, the summation in our definition of the moment of inertia must be converted to an integral. Because the definition involves the radial distance from a specific axis, the integrals are often best performed in cylindrical coordinates with the z-axis of the coordinate system identified with the axis of rotation. In this case, the sum can be converted to the following integral:
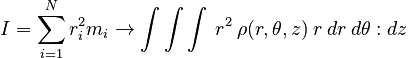
where ρ is the density of the object and the quantity:
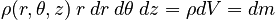
is the differential mass. Thus, the mass of the object can be expressed:
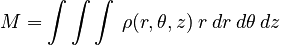
The total mass of the object is usually calculated to allow the moment of inertia to be expressed in a form not involving the density.
Integrals in Rectangular Coordinates
It is preferable in certain cases to perform the integral in rectangular coordinates instead, where the mass differential is:
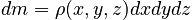
and the axis of rotation is again usually identified with the coordinate z-axis, giving:
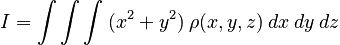
Summary of Commonly Used Moments of Inertia
Certain objects have simple forms for their moments of inertia. The most commonly referenced such objects are summarized in the table below. Note that the moments reported are only valid about the axis shown (the vertical line in all figures and in some cases shown as an "x" when more than one point of view is provided). In each case, the object has a total mass M and is assumed to be of uniform density.
The moment of inertia of composite objects formed of parts that are found in this table can often be found using the parallel axis theorem.
Description |
Illustration |
Moment of Inertia |
|---|---|---|
Thin Hoop or Hollow Cylinder of Radius R |
|
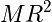 |
Disc or Solid Cylinder of Radius R |
|
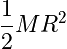 |
Thin Rod or Plane of Length L (rotated about center) |
|
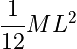 |
Thin Rod or Plane of Length L (rotated about edge) |
|
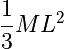 |
|
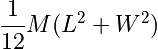 |
|
|
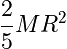 |
|
Thin Hollow Spherical Shell of Radius R |
|
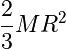 |










