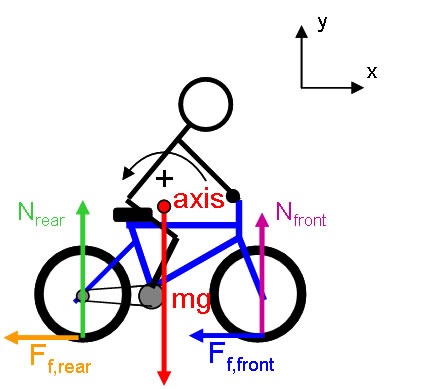
Part A
A cyclist sits on their bike at rest, supported only by the two wheels of the bike. The combined mass of the bike plus cyclist is 95 kg. The center of mass of the bike plus cyclist is 0.75 m above the ground, 0.42 m forward of the center of the rear wheel and 0.66 m behind the center of the front wheel. What is the size of the normal force exerted by the ground on each wheel?
Solution
System:
Cyclist plus bicycle are treated as a single rigid body.
Interactions:
External forces from the earth (gravity) and the ground (normal force and friction).
Model:
Single-Axis Rotation of a Rigid Body and Point Particle Dynamics.
Approach:
Diagrammatic Representation
We first sketch the situation and construct a coordinate system.
Mathematical Representation
We now write the equations of Newton's 2nd Law for the center of mass and of torque balance for the system. Since the system is at rest, we can put the axis wherever we choose. We select the point of contact of the rear wheel with the ground to remove an unknown from the torque equation.

Newton's Law for the x direction is trivial (0 = 0), so we have ignored it.
The torque equation immediately gives:

Force balance in the y direction then gives:

Part B
Suppose the cyclist described in Part A is coasting along at a constant speed when suddenly a car pulls out in front of them. The cyclist hits the brakes and locks both wheels (they stop rotating and begin to skid). The bike skids straight forward. If the cyclist and bike are decelerating at 0.55 g, what is the size of the normal force exerted by the ground on each wheel?
Solution
System:
Cyclist plus bicycle are treated as a single rigid body.
Interactions:
External forces from the earth (gravity) and the ground (normal force and friction).
Model:
Single-Axis Rotation of a Rigid Body and Point Particle Dynamics.
Approach:
Diagrammatic Representation
We again sketch the situation and construct a coordinate system.
Mathematical Representation
We now write the equations of Newton's 2nd Law for the center of mass and of torque balance about the center of mass for the bicycle.
The bicycle's center of mass is accelerating linearly in the negative x direction, but the bicycle is not rotating about its center of mass. Thus the torques about the center of mass must balance.
Because the bicycle is accelerating, the only point moving with the bike that can be chosen as an axis of rotation is the center of mass. Try repeating the problem with another axis (such as the point of contact of the front wheel with the ground) and you should find that the torques do not balance).

We have only three equations and four unknowns, but because the friction forces have the same moment arm about the center of mass, we can substitute for their sum. Thus, using torque balance, we can find:

We can then substitute for Nrear using Newton's 2nd Law for the y direction:

Note that ax is negative in our coordinate system.
Which means that:

Part C
What is the largest coefficient of kinetic friction allowed between the front tire and the ground if the rear tire is to remain on the ground during a skid?
Solution
System:
Cyclist plus bicycle are treated as a single rigid body.
Interactions:
External forces from the earth (gravity) and the ground (normal force and friction).
Model:
Single-Axis Rotation of a Rigid Body and Point Particle Dynamics.
Approach:
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>