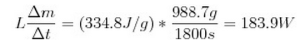1. Introduction
Source: "Atmosphere, Ocean, and Climate Dynamics: An Introductory Text" by John Marshall & Alan Plumb (2007).
Due to differential heating and conservation of energy, as well as the Earth’s rotation and conservation of momentum, there is a general trend of energy and momentum transportation from the equator to the poles. The transport of heat from the equator to the poles is not done through just one large circulation from the equator the poles, but rather a couple smaller circulations limited in size by the effects of the rotation of the Earth. More specifically, due to the rotation of the Earth, the general circulation in the atmosphere breaks down into two main regimes:
1) the Hadley Cell transporting heat from the equator to midlatitudes
2) Eddies transporting heat from the midlatitudes to the poles
In this study, through the use of rotating tank experiments and analysis of atmospheric data, we examined the dynamics and energy transport involved in both the Hadley Cell and midlatitude eddies to study the general circulation of the atmosphere.
2. Hadley Circulation
2.1) Introduction:
Hadley circulation works to transport heat from the warm equator to midlatitudes. The Hadley Cell consists of warm air rising from the equator and moving poleward to 30ºN and 30ºS where it falls to the surface. Due to the Coriolis effect which turns winds to the right in the Northern Hemisphere and to the left in the Southern Hemisphere, this air moves westward at the equator and eastward in the midlatitudes around 30ºN and 30ºS.
Source: "Atmosphere, Ocean, and Climate Dynamics: An Introductory Text" by John Marshall & Alan Plumb (2007).
2.2) Tank Experiment:
To better understand Hadley circulation, a tank experiment was set up to mimic these atmospheric conditions in a controlled environment. A metal container filled with ice was placed in the center of a slowly rotating circular tank. The low rotation rate, 1.28 RPM, and correspondingly low Rossby number (f = 2Ω) was chosen to replicate the low latitude regions where the Hadley Cell forms. Five thermometers (labelled A through E) were placed on the outside of the ice bucket and along the sides and bottom of the plastic tank, in order to measure the generated temperature gradient.
Surface Flow:
Particle tracking software was used to track the motion of paper dots on the surface of the water, in order to determine how velocity varied as a function of distance. The tracks of the five particles studied, along with the plot of their velocities (in meters per millisecond) as a function of distance from the center of the tank, are included below. These surface flows in the tank correspond to the trade winds on Earth.
Thermometers B (at the bottom of the outer wall of the ice bucket) and C (on the bottom of the tank) clearly measure much colder temperatures than sensors placed elsewhere. The maximum temperature gradient recorded between B and D, both near the bottom of the tank, is roughly 5.5K The maximum gradient found at the top of the tank is .5K. Averaging these gives an approximate temperature gradient of 3K over the 18 cm region, or 16.67 K/m.
We can recall the thermal wind equation for an incompressible fluid that we derived in our study of fronts:
This relationship relates the fluid horizontal speed in the tank to the tank’s rotation rate and temperature gradient. By plugging in the calculated value for the ∂T/∂r term into this thermal wind relation, we can try to approximate the velocity at the bottom of the tank. Integrating both sides of the equation, we find:
where u(z1) is the average velocity of a particle traveling on the surface of the water (8.5E-2 m/s for this experiment), u(z2) is the average velocity of a particle traveling near the bottom of the tank (assumed to be roughly 0), and Δz is the depth of water in the tank, here roughly 10cm. Plugging in these values, we find that the expected velocity of a particle traveling at the surface of the tank is:
This result is within the same order of magnitude as the observed values of roughly 8.5E-2 m/s. The slight differences are probably due to the inaccuracy of approximating the temperature gradient as the average of the difference at the top and the difference at the bottom. In reality, the temperature gradient was only observed at around the bottom fifth of the tank, but we didn’t have enough thermometers to measure this precisely.
2.2) Atmosphere:
As with the Hadley Cell tank experiment under low rotation described above, through atmospheric data analysis we will find that we can observe similar motions as observed in the tank near the equator, where Coriolis parameter is low and Earth’s rotation is felt very weakly.
For this study we analyzed zonally averaged data averaged over the years 1948-2015 to observe the general atmospheric circulation trends. NCEP reanalysis data from http://www.esrl.noaa.gov/psd/cgi-bin/data/composites/printpage.pl was plotted during both January and July to observe winters in both the Northern and Southern Hemispheres, during which the temperature gradients and the Hadley Cell circulation would be strongest.
We first plotted the zonally average temperature as shown below:
Note that the temperature gradient is stronger during winter (January in the Northern Hemisphere and July in the Southern Hemisphere). The sloping temperature surfaces shown are analogous to the sloping density surfaces we observed in the tank experiment in our study of fronts.
We next plotted the zonally averaged potential temperatures calculated using the expression we previously derived in our studies of fronts and convection:
Again we observe steeper temperature gradients in the Northern Hemisphere in January and in the Southern Hemisphere in July. Note that potential temperatures over the equatorial region are relatively constant, because there is more moisture in the air above the warmer equatorial regions, according to the Clausius-Clapeyron relation. Above the 200mb height, the shape of the isotherm curves reverses direction, because this is where the stratosphere begins.
Next, we plotted the zonally averaged zonal winds:
Here we observe zonal winds increasing in velocity with height. The strongest thermal winds are located above around 30ºN and 30ºS, where the temperature gradients are strongest. Again, the winds are stronger in the winter.
The correlation between the zonal winds and the potential temperature gradient are more easily observed when overlaying the two data plots:
To further reiterate the relationship between the winds and the temperature gradient, we can recall the expression for thermal wind we derived in our study of fronts in terms of temperature and in pressure coordinates:
We calculate the left hand side (LHS) and right hand side (RHS) of the expression at 30ºN in January and 30ºS in July where and when the zonal winds are strongest using the data from the zonally averaged plots above. The following values were used:
From the above calculations, we see that the the LHS and RHS for both January 30ºN and July 30ºS agree well, showing that the atmosphere obeys the thermal wind relation. We next plotted the zonally averaged vertical winds, given by the formula:
Where ω is negative, the air is rising.
In January, we observe air strongly rising over the equator and strongly sinking around 30ºN. In July, we observe air strongly rising over the equator and strongly sinking around 30ºS. Near the surface in both January and July, the maximums in upward vertical velocity are shifted slightly north of the equator, likely because the Northern Hemisphere has more land, which heats faster than water.
We next plotted the zonally averaged meridional winds where positive values correspond to northward moving winds:
In the January plot, high altitude winds move toward the North Pole from the equator to around 30ºN and low altitude winds move from 30ºN to the equator. The opposite pattern is observed in July.
Combining the vertical, meridional, and zonal wind data helps visualize the Hadley Cell circulation in the atmosphere. Here the meridional wind data is plotted over the vertical wind data, with the zonal components marked:
These plots show the Hadley Cell circulation in the Northern Hemisphere in January and in the Southern Hemisphere in July. We see similar but opposition motions between the two hemispheres.
Comparing the overlaid plot of meridional and vertical wind in January with the cartoon shown above we can think about the moisture in the atmosphere. Following the Clausius-Clapeyron relationship, the warm air around the equator is also moist. As this warm moist air rises above the equator, it cools adiabatically and the moisture condenses out of the air, creating precipitation and rainforests in equatorial regions. The air high in the atmosphere follows the Hadley Cell moving to around 30ºN. As the air descends over 30ºN, it adiabatically warms. However, this air is now dry since the moisture was condensed out earlier. Therefore this descent of warm dry air results in many dry desert regions around 30ºN and 30ºS around the world.
Overall, using zonally averaged data, we were able to clearly visualize the Hadley Cell circulation which works to transport heat from the equator to the midlatitudes around 30ºN and 30ºS.
3. Midlatitude Eddy Circulation
3.1) Introduction:
Source: http://visibleearth.nasa.gov/view.php?id=56236
The midlatitude eddy circulation, which we can observe surrounding the pole in the satellite image above, is important for heat transport in the atmosphere. Eddies occur at higher latitudes than the Hadley Cells and as estimates in the plot below show, are responsible for most of the heat transport required by the differential heating of the Earth. Once again we used a tank experiment and atmospheric data to study these eddies. Eddies occur in the midlatitudes, where Earth's rotation is more significant. Thus, to mimic eddies in our tank experiment, we used a high rotation rate and temperature gradient. To study eddies in the atmosphere, we used atmospheric data to study the heat transport involved in the midlatitude eddies.
Source: "Atmosphere, Ocean, and Climate Dynamics: An Introductory Text" by John Marshall & Alan Plumb (2007).
From the figure above, detailing heat transport by latitude, heat transport is at a maximum near 40ºN and S, where eddies occur. We integrate the zonally averaged heat flux due to eddies, to find the net poleward heat flux using the following equation,
where a is the Earth’s radius, is the latitude, cp is the specific heat, g is gravity, and 
We can notice a couple interesting things from these plots. In the January when the Northern Hemisphere is experiencing winter, we see two clear maximums of Northward heat flux. These could be because the temperature gradient is strongest during the winter. The maximums are located on coasts where there are strong land-sea interactions. The combination of the stronger gradient and land-sea interaction could result in more synoptic scale storms and more eddies, resulting in stronger heat flux in those regions. In July when the Northern Hemisphere is experiencing summer, we observe that the northward heat flux is stronger overall in the Northern Hemisphere as well as more uniform. In both January and July, we see strong southward heat flux in the Southern Hemisphere.
We next plotted the zonally averaged transient heat flux, averaged over the longitudes following:
These two plots again show poleward heat flux in both hemispheres. Both plots also show two maximums of heat flux, one at a higher and one at a lower altitude. Maximums in heat flux can be caused by either differences in velocity or in temperature. Higher in the atmosphere, the heat flux maximum could be driven by the strong velocity difference around the fast polar jet. Lower in the atmosphere, the heat flux maximum could be caused by the difference in temperature between the land and ocean.
Finally, we vertically integrate the zonally averaged transient heat flux and multiply by some constants to find the zonally and vertically integrated transient sensible energy flux using:
The maximum energy flux away is approximately 1PW and found around 40ºN and 40ºS because the eddy heat transport carries heat from the midlatitudes to the poles. The maximum energy flux from the atmosphere is actually about 4 PW in both North and South directions from around 40ºN and 40ºS. There is a discrepancy because we only calculated the sensible heat energy flux, neglecting the contributions from latent heat energy and potential energy that contribute to the 4PW plot.