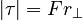Moment Arm
Also called the "lever arm", the moment arm is the distance of closest approach between the line of action of a force and the axis of rotation. It is used to compute the torque produced by the force about the axis of rotation.
Geometrical Definition
Illustration of the Method
The moment arm of a force about a specific axis of rotation can be found geometrically by constructing the force's line of action and then finding the shortest distance between the line of action and the axis. The procedure is shown in the figures below.
Vertical Forces
Given forces. |
Construct line of action for each. |
Find the shortest distance (shortest distance |
Horizontal Forces
Given forces. |
Construct line of action for each. |
Find the shortest distance (shortest distance |
General Angles
Given forces. |
Construct line of action for each. |
Find the shortest distance. |
Key Points
Some key points to remember:
- The moment arm must be perpendicular to the force.
- The moment arm is never perpendicular to the position vector that gives the point of application of the force with respect to the axis of rotation.
- The moment arm for vertical forces (e.g. gravity) is always perfectly horizontal.
- The moment arm for horizontal forces is always perfectly vertical.
- The moment arm must always be the shortest distance between the line of action and the axis, so it will always be less than or equal to the distance from the force's point of application to the axis of rotation.
Utility
Calculating Torque
The moment arm is often given the symbol:
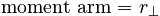
When the moment arm for a given force F about a chosen axis of rotation is known, the magnitude of the torque due to F about the axis is: