Thermodynamic variables are time averages of their microscopic counterparts. There is an enormous complexity with quantum mechanics, but there are few variables in thermodynamics. The two worlds are connected by posulating that

. The function on the right-side of the equation can be a many body wavefunction. It is possible to compute the wavefunction but it can be very complicated. A major postulate involves a weighted average over all possible states, and major pursuit is to find the probabilities,

, involved in the weighted average.
- Thermodynamic variables = time averages of their microscopic counterparts
-
 where
where
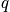 is the quantum number.
is the quantum number.
Major Postulate
A major postulate is that the the time average is the weighted average over all possible states the system can be in for a given set of boundary conditions.

If

is found, everything can be calculated. Any variable that can fluctuate can be determined in this way.
Math Review
Below is a listing of topics reviewed. Read McQuarrie Ch. 1 and see the online lecture notes for additional information
- Time-dependent Schrodinger equation
- wavefunction
- The time-dependence is removed when dealing with equilibrium.
- The solution without time-dependence is the stationary state.
- Hamiltonian
- The concept of degeneracy involves many states with the same energy
- Boundary conditions give specific\Psi (t), E
- Many-body problems are the sum of one-particle systems.
- Assume that degrees of freedom can be decoupled.
- Decouple the Hamiltonian and write as a sum.
- Energies of particular Hamiltonians can be superimposed
- Symmetry of wave functions is related to indistinguishability.
- Given an N particle wavefunction,

-

- Indistinguishable particles are dealt with in this course
- Given an N particle wavefunction,
Examples of Simple Quantum Mechanical Systems
Write what interactions are assumed and solutions.
Particle in a 1-D Infinite Well Potential
A physical example of a 1-D infinite well potential is a particle in a box. Below is a schematic of the potential.
Write the Hamiltonian,
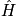
, define the potential, and find the energy eigenvalues.

<P></P>

<P></P>
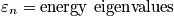
<P></P>

Simple Harmonic Oscillator (1-D)
In the case of a simple harmonic oscillator, a system moved from equilibrium feels a restoring force.
The energy eigenvalues are discrete.
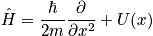
<P></P>

<P></P>

The Concept of Degeneracy
Hydrogen Atom
Consider the hydrogen atom. The energy eigenvalues are proportional to the inverse of the square of the principal quantum number,

. For every
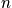
, there are

,
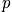
, and

states that are dependent on the angular momentum. They are all degenerate in energy, but there are different wavefunctions associated with each. Consider a table of degeneracy. The degeneracy,
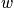
, is equal to
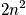
, where the factor of two is due to spin.

<P></P>

<P></P>

 |
 |
 |
|---|---|---|
 |
 |
 |
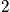 |
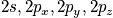 |
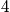 |
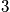 |
 |
 |


Degeneracy of one particle in a 3-D Infinite Well Potential
This is a generalization of the one-dimensional case. Assume that the three directions are independent, and write the energy eigenvalues.



How many ways can we get the same
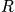
? Consider an example of

. Create a table of possibilities and find that
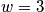
.
 |
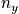 |
 |
|---|---|---|
1 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
1 |
Generalized for any R in 3-D
How do we find the generalized
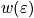
in 3D? Show is two dimensions and envision in three dimensions. Degeneracy is how many dots land on the arc of R in the n space. Below is a diagram in the case of two dimensions. Look at positive vales of
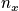
and

. For small quantum numbers, there is an irratic step function, but the function is smooth for large functions.
The degeneracy in three dimensions is equal to the number of points on the sphere with radius R in the first quadrant.
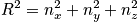
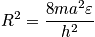
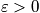

When

or
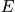
is large, it can be treated as a continuous variable. Determine the number of lattice points between

and

or

and

. Look at the number of points within the sphere; consider the number of points with energy less than

. If the number of points is dense, it can be set to the volume, and below is an expression for

, which is defined as the number of points within
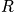
.


The number of states in a slice, or the number of states between

and

, is of interest. A formula is below for the number of states that become available when increasing energy by a small amount. There is an assumption that
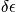
is very small, and there is a Taylor expansion.

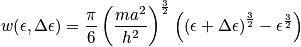


Look at the order of magnitude of this. Consider just the kinetic energy in three dimensions. The formula for kinetic energy is

. Temperature can't be assigned to just one particle. Consider one particle in contact with heat bath, a gas particle in a box.

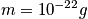


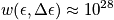
There is a huge number of additional points. The number of states that can be accessed is enormous. The numbers are very dense using room temperature. When calculating with interacting particles the results are about the same.
Summary
- for small R --> w is erratic
- for large R --> w is more smooth
For 3D case
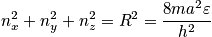
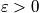

Additional math topics
A listing is below of additional math topics covered. Additional information is posted at thecourse website.
- Average of

- Mean of a function
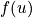
-
 moment of distribution
moment of distribution -
 central moment of a distribution
central moment of a distribution - Integration of function with probability density
- Gaussian distribution
- Stirling's approximation
- Binomial/multinomial distribution
October 20, 2006