Find the moment of inertia of a solid rectangular block of uniform density ρ with side lengths L, W and h rotated about an axis parallel to the sides of length h (perpendicular to the faces of dimensions L by W) and passing through the center of the block.

Solution

System, Interactions & Model: Not applicable. We will solve this problem using the defintion of moment of inertia.

Approach: The object does not possess an axial symmetry and so cylindrical coordinates will be unwieldy here. Instead, we use rectangular coordinates with the z-axis placed atop the axis of rotation. We select the x-axis to point parallel to the sides of length L and the y-axis to point parallel to the sides of length W.

The form of the integral for the moment of inertia in rectangular coordinates is:

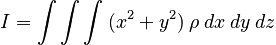
Because we have chosen our axes parallel to the sides of the rectangle, the limits are straightforward:

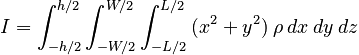
Evaluating the integrals one by one gives:

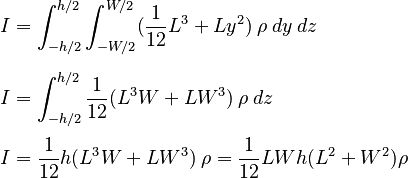
The mass of the block is of course:

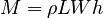
so:

html: Security restricted macro is not allowed. An edit restriction is required that matches the macro authorization list.

<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>