A ball hits a bar and sticks to it.

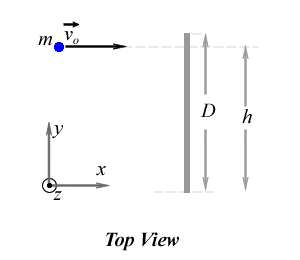
A uniform bar of mass M and length d is initially at rest on a horizontal and frictionless table. A ball of mass m and very small radius is moving towards the bar with speed v_o, hits and sticks to the bar at a distance h measured from on end of the bar. The bar is not attached to the table and its moment of inertia with respect to its center of mass is known to be I_cm. The goal of the problem is to find the angular velocity and the velocity of the bar's center of mass.

.
Solution:
System: The ball is treated as a point mass and the bar as a rigid body with its mass uniformly distributed. The external forces on the system are the result of the interactions between the elements of the system and the Earth (gravitational force on ball and on bar) and with the table's surface (as there is no fricition it is the normal force exerted by the surface on the ball and on the bar).
Model: 1-D Angular Momentum and Angular Impulse and Linear Momentum and Impulse.

Approach:

The motion of the objects before and after the collision is in the surface of the table, in the _(x,y)_ plane. After the collision the ball-bar system will translate to the right and rotate counter-clockwise about its center of mass. The system's center of mass is not at the center of the bar but at a point between the ball and the center of the bar. 

To solve the problem realize that the sum of the external forces exerted on the system is zero and the sum of the torques due to the external forces is also zero about any given point. The external forces exerted on the ball are the gravitational force and the normal force. Both forces are applied at the ball's center of mass. Because there is no motion of the ball in the direction perpendicular to the table's surface (z-axis) these two forces add to zero, therefore they have the same magnitude and opposite direction. As a consequence, the torques due to these two forces about any given point have the same magnitude and opposite direction, therefore they also add to zero. The external forces acting on the bar are gravitational force and the normal force exerted by the the force exerted by the surace and the

The forces acting on the elements of the system are the gravitational force on the ball and on the bar and the contact force exerted by the table's surface on the ball and on the bar. Because there is no friction thesi contact force has only one component p[erpendicular to the surface.
Modeling the objects:
Ball:
Because the ball has a small radius we will neglect any possible rotation of the ball an we will treat it as a point mass translating with initiall speed v_o.
Bar:
We will treat the bar as a rigid body with its mass uniformly distributed therfore, its center of mass is in the middle of the bar.
Modeling the interactions:
Ball:
The ball interacts with the Earth, the surface and the bar. As a resullt of these three interactions there are three forces acting on it:
#The gravitational force exerted by the Earth on the ball, F_EonBall. This is an external force and is applied at the ball's center of mass.
#The contact force exerted by the ground on the ball. Because there is no friction this force has only one component perpendicular to the surface, F_{N on Ball}. This force is an external force and is applied at the ball's center of mass.
#The force exerted by the bar on the ball, F_{Bar on Ball}. This force is an internal force and is applied at th eball's center of mass. It is the action reaction pair of the force exerted by the ball on the bar.
Bar:
The bar interacts with the Earth, the surface and the ball. As a resullt of these three interactions there are three forces acting on it:
#The gravitational force exerted by the Earth on the bar, F_{E on Bar}. This force is an external force and is applied at the bar's center of mass.
#The contact force exerted by the ground on the bar. Because there is no friction this force has only one component perpendicular to the surface, F_{N on Bar}. This force is an external force and is applied at the bar's center of mass.
#The force exerted by the ball on the bar, F_{Ball on Bar}. This force is an internal force and is applied at the point where the ball hits the bar, which is the point at a distance h from the lower end of the bar.

Because there is no motion of the ball and the rod in the direction perpendicular to the table's surface then Newton's second law applied on the ball and the stick implies that F_{E on Ball}+ F_{N on Ball} = 0 and F_{E on Bar}+ F_{N on Bar} = 0