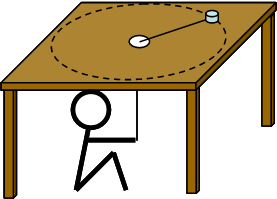
A small object with a mass of 0.250 kg has been attached to a massless string, and is moving in a circle on a perfectly level frictionless tabletop. The string passes through a hole in the center of the table, and is held by a person. Suppose that initially the mass is rotating with an angular speed of 15.0 rad/s around a circle of radius 0.400 m. The person then pulls the string in such a way as to reduce the radius of the circle at a constant rate. The person stops reducing the radius when the object is making a circle of radius 0.200 m. How much work did the person do in the course of reducing the radius of the circle?
Solution
We will approach the problem in two ways. First, we will use the change in mechanical energy to obtain the answer in a straightforward manner. We will then compare our answer to that obtained using the (considerably more complicated) method of computing the integral of the force times displacement along the path.
Method 1
System:
Interaction:
Model:
Approach:
Consider the Energy
The table is level, so the [gravitational potential energy] will be constant. We can set it to zero by taking the height of the tabletop to be zero. The normal force is perpendicular to the motion of the object and so does no work. The only force capable of performing work on the object is the tension, which is equal to the force from the person pulling on the string. Thus, the work done by tension will equal the work done by the person. This work can be computed by finding the change in mechanical energy of the object:
\begin
[ W^
+ E_
= E_
]\end
or, since the height of the object is constant throughout the motion and no spring is present:
\begin
[ W^
= E_
- E_
Unknown macro: {i}= K_
- K_
]\end
Because the object can be considered to be moving in pure rotation about the center of the circle, we can compute its kinetic energy using the rotational formula:
\begin
[ K = K_
= \frac
]\end
For a point particle,
\begin
[ I = mr^
]\end
and so:
\begin
[ W = \frac
m\left(r_
^
\omega_
^
- r_
Unknown macro: {i}^
\omega_
^
\right)]\end
Note that we have assumed the mass is constant, but we cannot assume the angular speed is constant.
Consider the Angular Momentum
We cannot yet substitute into the equation obtained by considering the object's energy. We do already have the initial and final radius of the motion, but we do not yet have the angular speed. To find it, we consider the torque on the system. We choose the natural location for the axis by locating it at the center of the circle.
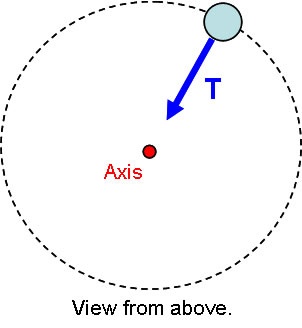
With this choice, we can see that there is zero net torque on the system, since the moment arm for the tension is zero. With the net torque equal to zero, we are in the special case of constant angular momentum, so:
\begin
[ I_
= I_
]\end
By using the formula for the moment of inertia of a point particle, we can show:
\begin
[ \omega_
= \omega_
\left(\frac{r_{i}}{r_{f}}\right)^
]\end
Substituting into the work-energy theorem then gives:
\begin
[ W = \frac
mr_
^
\omega_
^
\left(\frac{r_
^{2}}{r_
^{2}} - 1\right) =\mbox
]\end
