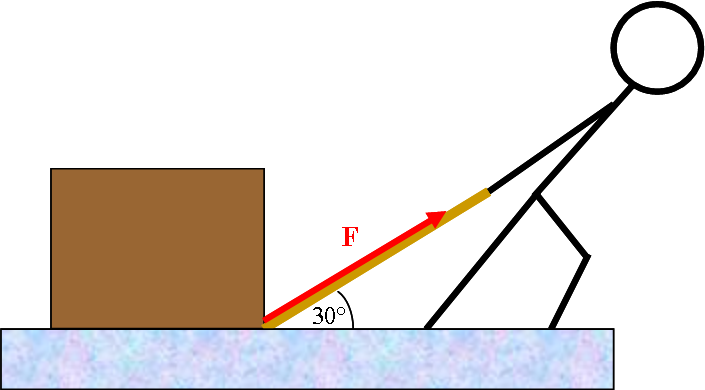
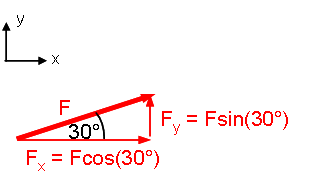
Part A

Solution

System:

Interactions:

Model:

Approach:

Diagrammatic Representation

Before writing Newton's 2nd Law for the x direction, we choose coordinates and break the applied force F into x- and y-components:

Mathematical Representation

Using the free body diagram, we can write the relevant x-component of Newton's 2nd Law:

\begin{large}\[ \sum F_{x} = F\cos\theta = ma_{x}\] \end{large}

Solving for F:

\begin{large}\[ F = \frac{ma_{x}}{\cos\theta} = \mbox{34.6 N}\]\end{large}

Part B

A person pulls a box of mass 15 kg along a smooth floor by applying a force F at an angle of 30° above the horizontal.. The box accelerates horizontally at a rate of 2.0 m/s². What is the magnitude of F?

Solution

System:

Interactions:

Model:

Approach:

Diagrammatic Representation

Before writing Newton's 2nd Law for the x direction, we choose coordinates and break the applied force F into x- and y-components:

Mathematical Representation

The free body diagram implies:

\begin{large}\[ \sum F_{x} = F\cos\theta = ma_{x}\] \end{large}

Solving for F:

\begin{large}\[ F = \frac{ma_{x}}{\cos\theta} = \mbox{34.6 N}\]\end{large}