Part A

A person pushes a box of mass 15 kg along a floor by applying a perfectly horizontal force F. The box accelerates horizontally at a rate of 2.0 m/s².

Solution

System:

Interactions:

Model:

Approach:

Diagrammatic Representation

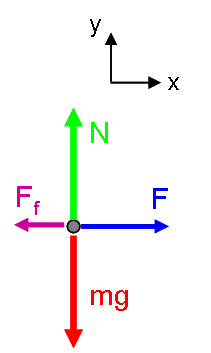
The free body diagram for this situation is:

Mathematical Representation

With this free body diagram, Newton's 2nd Law can be written:

\begin{large}\[ \sum F_{x} = F - F_{f} = ma_{x} \]
\[ \sum F_{y} = N - mg = ma_{y} = 0 \]\end{large}

where we have assumed that the y acceleration is zero because the box is sliding along a horizontal floor, not moving upward or downward. This realization is important, because we know F_f = μN. Thus, because the y acceleration is zero, we can solve Newton's 2nd Law in the y direction to yield:

\begin{large}\[ N = mg\]\end{large}

so that:

\begin{large}\[ F = ma_{x}+F_{f} = ma_{x} + \mu_{k}N = ma_{x} + \mu_{k}mg = \mbox{96 N} \] \end{large}

Part B

A person pushes a box of mass 15 kg along a floor by applying a perfectly horizontal force F. The box moves horizontally at a constant speed of 2.0 m/s in the direction of the person's applied force. Assuming the coefficient of kinetic friction between the box and the ground is 0.45, what is the magnitude of F?

System, Interactions and Model:

Approach:

Just as above, [Newton's 2nd Law|Newton's Second Law] can be written:

{latex}\begin{large}\[ \sum F_{x} = F - F_{f}= ma_{x} \]
\[ \sum F_{y} = N - mg = 0\] \end{large}{latex}

This time, however, the _x_ acceleration is also zero, since the box maintains a constant speed.  This implies:

{latex}\begin{large}\[ F = ma_{x} + F_{f} = F_{f} = \mu_{k}mg = \mbox{66 N} \] \end{large}{latex}