Part A
null
A person pushes a box of mass 15 kg along a floor by applying a perfectly horizontal force F. The box accelerates horizontally at a rate of 2.0 m/s2. Assuming the coefficient of kinetic friction between the box and the ground is 0.45, what is the magnitude of F?
System: Box as point particle subject to external influences from the person (applied force) the earth (gravity) and the floor (normal force and friction).
Model: Point Particle Dynamics.
Approach: The free body diagram for this situation is:
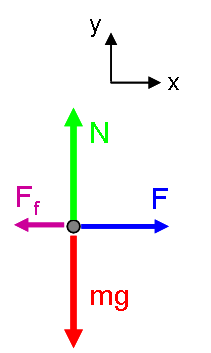
With this free body diagram, Newton's 2nd Law can be written:
\begin
[ \sum F_
= F - F_
= ma_
]
[ \sum F_
= N - mg = ma_
= 0 ]\end
where we have assumed that the y acceleration is zero because the box is sliding along a horizontal floor, not moving upward or downward. This realization is important, because we know Ff = μN. Thus, because the y acceleration is zero, we can solve Newton's 2nd Law in the y direction to yield:
\begin
[ N = mg]\end
so that:
\begin
[ F = ma_
+F_
= ma_
+ \mu_
N = ma_
+ \mu_
mg = \mbox
] \end
Part B
A person pushes a box of mass 15 kg along a floor by applying a perfectly horizontal force F. The box moves horizontally at a constant speed of 2.0 m/s in the direction of the person's applied force. Assuming the coefficient of kinetic friction between the box and the ground is 0.45, what is the magnitude of F?
System and Model: As in Part A.
Approach: Just as above, Newton's 2nd Law can be written:
\begin
[ \sum F_
= F - F_
= ma_
]
[ \sum F_
= N - mg = 0] \end
This time, however, the x acceleration is also zero, since the box maintains a constant speed. This implies:
\begin
[ F = ma_
+ F_
= F_
= \mu_
mg = \mbox
] \end