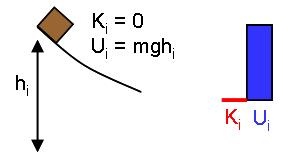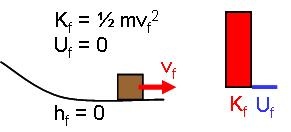Consider three ways to get a block from height hi down to height hf = 0: dropping the block straight down through the air (freefall), sliding the block down a frictionless ramp, or sliding the block along a frictionless track. The options are illustrated above.
Part A
Assuming that the block starts from rest, what is the final speed of the block as it reaches the ground in each case?
Solution
We begin by solving all three problems using mechanical energy. We will then re-solve the first two cases using the equations of kinematics and dynamics to illustrate the agreement between the methods.
Method 1
System:
Block as point particle plus the earth as a rigid body with infinite mass.
Interactions:
In each case, there is a conservative gravitational interaction between the block and the earth which will provide a gravitational potential energy. In the final two cases (the ramp and the track) the block is also subject to a non-conservative normal force from the surface upon which it travels. In each case, however, the normal force does no work, since it is always perpendicular to the direction of the block's travel (the block is always moving parallel to the surface and the normal force is, by definition, perpendicular to the surface). Thus, in all three cases, the non-conservative work is zero.
Model:
Mechanical Energy, External Work, and Internal Non-Conservative Work.
Approach:
Diagrammatic Representation
Since the non-conservative work is zero, the mechanical energy will be constant:
Unknown macro: {latex} \begin
Unknown macro: {large} [ E_
Unknown macro: {i}
= E_
Unknown macro: {f}
]\end
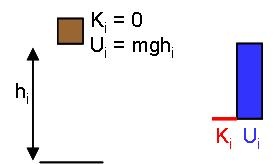
In each case, the initial-state final-state diagram and energy bar graphs will be:
|
Initial |
Final |
Drop |
|

|
Ramp |
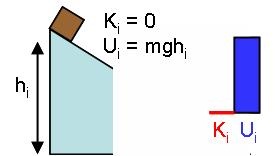
|
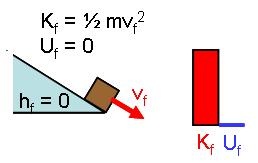
|
Track |
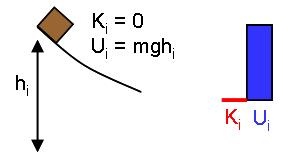
|
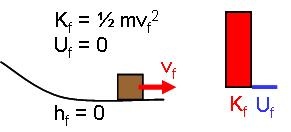
|
Mathematical Represenation
In each case, the constant energy relationship is:
Unknown macro: {latex} \begin
Unknown macro: {large} [ mgh_
Unknown macro: {i}
= \frac
Unknown macro: {1}
Unknown macro: {2} mv_
Unknown macro: {f}
^
]\end
giving:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {f}
= \sqrt{2gh_{i}} ]\end
independent of the path taken from hi to the zero height level.
Method 2
System:
Box as point particle.
Interactions:
External influences from the earth (gravity) and for the block on the ramp, the ramp provides a normal force.
Model:
One-Dimensional Motion with Constant Acceleration and Point Particle Dynamics.
Approach:
For the drop and the ramp, we can recover the same result using kinematics.
The Drop
For the drop, if we set up coordinates with the positive y direction pointing vertically, the acceleration will be ay = – g, so that the most straightforward approach is to use the Law of Change:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {y,f}
^
Unknown macro: {2} = v_
Unknown macro: {y,i}
^
+ 2a_
Unknown macro: {y}
\Delta y ] \end
Using the givens:
Unknown macro: {latex} \begin
Unknown macro: {large} [ y_
][ y_
Unknown macro: {f}
= 0] [v_
Unknown macro: {y,i}
= 0][ a_
Unknown macro: {y}
= - g]\end
Substituting these givens yields:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {y,f}
= \sqrt{2gh_{i}} ]\end
The Ramp
For the ramp, we tilt the coordinates to place the x-axis along the ramp surface. The free body diagram for the box is shown below.
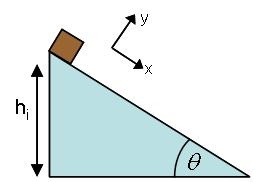
|
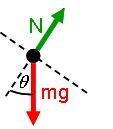
|
Coordinates |
Free Body Diagram |
The diagram implies that Newton's 2nd Law for the x direction takes the form:
Unknown macro: {latex} \begin
Unknown macro: {large} [ \sum F_
Unknown macro: {x} = mg\sin\theta = ma_
]\end
giving:
Unknown macro: {latex} \begin
Unknown macro: {large} [ a_
Unknown macro: {x}
= g\sin\theta]\end
With the acceleration determined, we turn to kinematics to find the final velocity. We have the givens:
Unknown macro: {latex} \begin
Unknown macro: {large} [ x_
Unknown macro: {i}
= 0][ x_
Unknown macro: {f}
= \frac{h_{i}}
Unknown macro: {sintheta}
] [v_
Unknown macro: {x,i}
= 0][a_
Unknown macro: {x}
=g\sin\theta] \end
We then substitute into the Law of Change for one-dimensional motion:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {x,f}
^
Unknown macro: {2} = v_
Unknown macro: {x,i}
^
+ 2a_
Unknown macro: {x}
\Delta x]\end
Substituting the givens yields:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {x,f}
= \sqrt{2gh_{i}}]\end
deck: com.atlassian.confluence.macro.MacroExecutionException: java.lang.NullPointerException
Part B
In Part A, we showed that the speed of the blocks at the end of their trip is independent of the path taken from one height to another. This equality does not mean, however, that the trips are identical in every way. The time taken to complete the trip will depend upon the details of the path. We can show this by calculating the time taken to complete the trip for the case of the dropped box and the box sliding down the ramp using kinematics.
Solution
System:
The box as point particle.
Interactions:
External influences from the earth (gravity) and for the block on the ramp, the ramp provides a normal force.
Model:
One-Dimensional Kinematics with Constant Acceleration.
Approach:
One direct way (of several) to obtain the time is to use the Law of Change:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {f}
= v_
Unknown macro: {i}
+ at]\end
which gives:
Unknown macro: {latex} \begin
Unknown macro: {large} [ t_
Unknown macro: {rm drop}
= \frac{\sqrt{2gh_
Unknown macro: {i} }}
Unknown macro: {g}
= \sqrt{\frac{2h_{i}}{g}}][t_
Unknown macro: {rm ramp}
= \frac{\sqrt{2gh_
}}
Unknown macro: {gsintheta}
= \frac
Unknown macro: {1}
Unknown macro: {sintheta}
\sqrt{\frac{2h_{i}}{g}} ]\end
Error rendering macro 'deck'
java.lang.NullPointerException