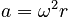The acceleration directed toward the center of rotation that results from the change in direction (not magnitude) of the velocity when an object is in circular motion.
Form of the Acceleration
We can derive the form of the acceleration required to produce uniform circular motion. We begin by writing the position of an object undergoing uniform circular motion as a function of time. We can, with complete generality, choose a coordinate system that has its origin at the center of the circle and which aligns the x-y plane with the plane of the circle. Further, we can choose to look at the motion from the side which makes it clockwise. Finally, we can set our clocks such that t = 0 occurs when the object intersects the positive x-axis. With these choices, the form of the position as a function of time will be:
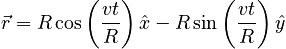
where v is the speed of the motion and R is the radius, both of which are constants for uniform circular motion.
We can now obtain the acceleration by performing two derivatives with respect to time. The first
derivative gives the velocity:
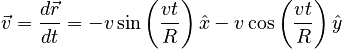
and the second gives the acceleration:
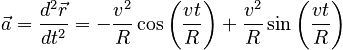
Comparing the expression for the acceleration with our original expression for the position, we see that:
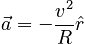
Comparing the expressions found for r, v and a leads to the following picture:
Note that the acceleration points at all times toward the center of the circle (which is the reason for the name centripetal) and is perpendicular to the velocity. The acceleration has magnitude:
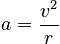
It is important to note that the equation relates the magnitude of the velocity to the magnitude of the acceleration. Both the acceleration and the velocity will be constantly changing directions during the motion.
Centripetal Acceleration in Angular Variables
Using a regular x and y coordinate system is awkward when describing circular motion. It is simpler to instead describe the motion in terms of an angular position. Suppose that we describe the position of the object executing circular motion by giving its angle θ measured counterclockwise from the x-axis. It will turn out to be most useful to measure the angle in radians. This angular position will be constantly changing as the object moves around the circle. Thus, we can define its time derivative, which will be called the angular velocity ω:
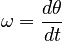
For the case of uniform circular motion, this angluar velocity will have a constant magnitude equal to 2 π radians per period T. Thus:
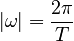
We can now find a relationship between the magnitude of the linear velocity as the particle goes around the circle and the angular velocity. The x and y components of the linear velocity were given above. By using the Pythagorean theorem and the fact that sin 2θ + cos 2θ = 1, you can show from those expressions that
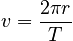
This expression is also clearly true since 2 π r is the distance of the circle's circumference and T is the time taken to move around 1 circumference of the circle.
Thus, we have the relationship:
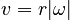
This relationship means that we can write the centripetal acceleration in another way: